题目内容
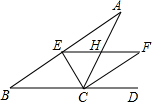 已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.考点:等腰三角形的判定与性质,平行线的性质
专题:证明题
分析:由角平分线的定义和平行的性质可得到∠ECA=∠HEC,从而可得到EH=HC,同理可得到HC=HF,可得出结论.
解答:证明:
∵EF∥BC,
∴∠HEC=∠ECB,
∵CE平分∠ACB,
∴∠ECB=∠ECA,
∴∠ECA=∠HEC
∴EH=HC,
同理HC=HF,
∴EH=HF.
∵EF∥BC,
∴∠HEC=∠ECB,
∵CE平分∠ACB,
∴∠ECB=∠ECA,
∴∠ECA=∠HEC
∴EH=HC,
同理HC=HF,
∴EH=HF.
点评:本题主要考查等腰三角形的判定及平行线的性质,由条件得到∠ECA=∠HEC是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
下列说法中正确的是( )
| A、a和0都是单项式 | ||
| B、多项式-3a2b+7a2b2-2ab+l的次数是3 | ||
C、单项式-
| ||
| D、x2+2xy-y2可读作x2、2xy、y2的和 |
若x2+x-1=0,则3x2+3x-6的值等于( )
| A、-3 | B、3 | C、-5 | D、5 |
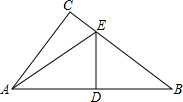 如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.
如图,在△ABC,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAE=∠B+40°,求∠AEB的度数.
 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题: