题目内容
10. 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C.(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标.
分析 (1)由抛物线解析式y=-x2-2x+3,令y=0求得x即可;
(2)设点D坐标为(-1,yD),根据三角形的面积公式以及△ACD与△ACB面积相等,即可得出关于yD含绝对值符号的一元一次方程,解方程即可得出结论;
解答 解:(1)令y=0代入y=-x2-2x+3,
∴-x2-2x+3=0,
解得:x=1或x=-3,
∴A(-3,0),B(1,0);
(2)如图所示.
∵A(-3,0),B(1,0),
∴OA=OC,△AOC为等腰直角三角形.
设AC交对称轴x=-1于F(-1,yF),
由点A(-3,0)、C(0,3)可知直线AC的解析式为y=x+3,
∴yF=-1+3=2,即F(-1,2).
设点D坐标为(-1,yD),
则S△ADC=$\frac{1}{2}$DF•AO=$\frac{1}{2}$×|yD-2|×3.
又∵S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×[1-(-3)]×3=6,且S△ADC=S△ABC,
∴$\frac{1}{2}$×|yD-2|×3.=6,解得:yD=-2或yD=6.
∴点D的坐标为(-1,-2)或(-1,6).
点评 本题考查了抛物线与x轴的交点问题,解题的关键是找出关于yD含绝对值符号的一元一次方程.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
6. 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )| A. | 体育场离张强家2.5千米 | |
| B. | 张强在体育场锻炼了15分钟 | |
| C. | 体育场离早餐店4千米 | |
| D. | 张强从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
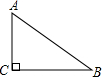 如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上.
如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上. 如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.
如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为11 cm.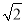 的倒数是( )
的倒数是( )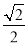 B.
B. 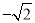 C.
C. 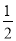 D.
D. 