题目内容
20．已知x1、x2是方程x2+7x-5=0的两实数根，求$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值．分析 先根据根与系数的关系求出x1+x2与x1x2的值，再代入代数式进行计算即可．
解答 解：∵x1、x2是方程x2+7x-5=0的两实数根，
∴x1+x2=-7，x1x2=-5，
∴$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{（{x}_{2}+{x}_{1}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{49+10}{-5}$=-$\frac{59}{5}$．
点评 本题考查的是根与系数的关系，熟记一元二次方程的根与系数的关系是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．化简|x-5|-|2x-13|（5＜x＜6）得（ ）
| A． | -x+8 | B． | 3x-18 | C． | -3x+18 | D． | x-8 |
如图，要使得△ABC≌△DFE，已知∠A=∠D，AB=DF，根据AAS还需要的条件是∠ACB=∠DEF．
10．如图：在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，可得到点P3，此时AP3=3+$\sqrt{3}$；…，按此规律继续旋转，直到得到点P2015为止，则AP2015=（ ）
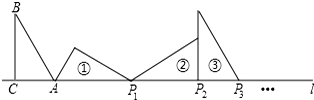
| A． | 2015+672$\sqrt{3}$ | B． | 2013+671$\sqrt{3}$ | C． | 2013+672$\sqrt{3}$ | D． | 2015+671$\sqrt{3}$ |