题目内容

已知：∠A为锐角，sinA=数学公式，则tanA=________．


分析：根据sinA=，设出关于两边的代数表达式，再根据勾股定理求出第三边长的表达式即可推出tanA的值．
解答：由sinA==知，如果设a=x，则c=3x，
结合a2+b2=c2得b=2x．
∴tanA===．
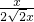故答案为：．
点评：求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值．
练习册系列答案
相关题目
已知：∠A为锐角，且sinA=
817
，则tanA的值为
 
．
已知：∠A为锐角，sinA=
13
，则tanA=
 
．
（2013•湛江）阅读下面的材料，先完成阅读填空，再按要求答题：
sin30°=
1
2
，cos30°=
3
2
，则sin230°+cos230°=
1
1
；①
sin45°=
2
2
，cos45°=
2
2
，则sin245°+cos245°=
1
1
；②
sin60°=
3
2
，cos60°=
1
2
，则sin260°+cos260°=
1
1
．③
…
观察上述等式，猜想：对任意锐角A，都有sin2A+cos2A=
1
1
．④
（1）如图，在锐角三角形ABC中，利用三角函数的定义及勾股定理对∠A证明你的猜想；
（2）已知：∠A为锐角（cosA＞0）且sinA=
3
5
，求cosA．
已知α，β均为锐角，且tanα=
1
2
，tanβ=
1
3
，求α+β的度数．
已知：∠A为锐角，且cosA≥
1
2
，则（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网