题目内容
（2013•湛江）阅读下面的材料，先完成阅读填空，再按要求答题：sin30°=
| 1 |
| 2 |
| ||
| 2 |
1
1
；①sin45°=
| ||
| 2 |
| ||
| 2 |
1
1
；②sin60°=
| ||
| 2 |
| 1 |
| 2 |
1
1
．③…
观察上述等式，猜想：对任意锐角A，都有sin2A+cos2A=
1
1
．④（1）如图，在锐角三角形ABC中，利用三角函数的定义及勾股定理对∠A证明你的猜想；
（2）已知：∠A为锐角（cosA＞0）且sinA=
| 3 |
| 5 |
分析：①②③将特殊角的三角函数值代入计算即可求出其值；
④由前面①②③的结论，即可猜想出：对任意锐角A，都有sin2A+cos2A=1；
（1）过点B作BD⊥AC于D，则∠ADB=90°．利用锐角三角函数的定义得出sinA=
，cosA=
，则sin2A+cos2A=
，再根据勾股定理得到BD2+AD2=AB2，从而证明sin2A+cos2A=1；
（2）利用关系式sin2A+cos2A=1，结合已知条件cosA＞0且sinA=
，进行求解．
④由前面①②③的结论，即可猜想出：对任意锐角A，都有sin2A+cos2A=1；
（1）过点B作BD⊥AC于D，则∠ADB=90°．利用锐角三角函数的定义得出sinA=
| BD |
| AB |
| AD |
| AB |
| BD2+AD2 |
| AB2 |
（2）利用关系式sin2A+cos2A=1，结合已知条件cosA＞0且sinA=
| 3 |
| 5 |
解答：解：∵sin30°=
，cos30°=
，
∴sin230°+cos230°=（
）2+（
）2=
+
=1；①
∵sin45°=
，cos45°=
，
∴sin245°+cos245°=（
）2+（
）2=
+
=1；②
∵sin60°=
，cos60°=
，
∴sin260°+cos260°=（
）2+（
）2=
+
=1．③
观察上述等式，猜想：对任意锐角A，都有sin2A+cos2A=1．④
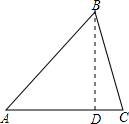（1）如图，过点B作BD⊥AC于D，则∠ADB=90°．
∵sinA=
，cosA=
，
∴sin2A+cos2A=（
）2+（
）2=
，
∵∠ADB=90°，
∴BD2+AD2=AB2，
∴sin2A+cos2A=1．
（2）∵sinA=
，sin2A+cos2A=1，∠A为锐角，
∴cosA=
=
．
| 1 |
| 2 |
| ||
| 2 |
∴sin230°+cos230°=（
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∵sin45°=
| ||
| 2 |
| ||
| 2 |
∴sin245°+cos245°=（
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵sin60°=
| ||
| 2 |
| 1 |
| 2 |
∴sin260°+cos260°=（
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
观察上述等式，猜想：对任意锐角A，都有sin2A+cos2A=1．④
（1）如图，过点B作BD⊥AC于D，则∠ADB=90°．∵sinA=
| BD |
| AB |
| AD |
| AB |
∴sin2A+cos2A=（
| BD |
| AB |
| AD |
| AB |
| BD2+AD2 |
| AB2 |
∵∠ADB=90°，
∴BD2+AD2=AB2，
∴sin2A+cos2A=1．
（2）∵sinA=
| 3 |
| 5 |
∴cosA=
1-(
|
| 4 |
| 5 |
点评：本题考查了同角三角函数的关系，勾股定理，锐角三角函数的定义，比较简单．
练习册系列答案
相关题目
22、阅读下题及证明过程：