题目内容
6.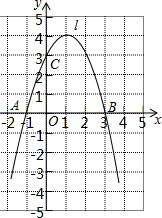 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标.
分析 (1)把A,B,C三点坐标代入抛物线解析式求出a,b,c的值,确定出抛物线解析式即可;
(2)做出C关于直线x=1的对称点C′,连接AC′,与直线x=1交于点P,此时△PAC的周长最小,求出此时直线AC′解析式,即可确定出P坐标.
解答 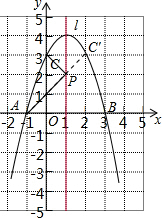 解:(1)把A(-1,0)、B(3,0)、C(0,3)代入抛物线解析式得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解:(1)把A(-1,0)、B(3,0)、C(0,3)代入抛物线解析式得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:a=-1,b=2,c=3,
则抛物线解析式为y=-x2+2x+3;
(2)找出C关于直线x=1的对称点C′(2,3),连接AC′,与直线x=1交于点P,此时△PAC的周长最小,
设直线AC′解析式为y=kx+b,
把A(-1,0),C′(2,3)代入得:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=3}\end{array}\right.$,
解得:k=1,b=1,
∴直线AC′解析式为y=x+1,
把x=1代入得:y=2,
则P坐标为(1,2).
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法正确的是( )
| A. | 要调查人们对“低碳生活”的了解程度,宜采用普查方式 | |
| B. | 一组数据3,4,4,6,8,5的众数和中位数都是3 | |
| C. | 必然事件的概率是100%,随机事件的概率是50% | |
| D. | 甲组数据的方差S甲2=0.13,乙组数据的方差S乙2=0.04;则乙组数据比甲组数据稳定 |
1.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m、n,则二次函数y=x2+mx+n的图象与x轴没有公共点的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{17}{36}$ | D. | $\frac{1}{2}$ |
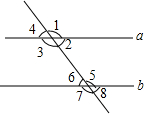 如图所示,直线c截直线a,b,现给出下列以下条件:①∠4=∠8;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°.其中能说明a∥b的条件有( )个.
如图所示,直线c截直线a,b,现给出下列以下条件:①∠4=∠8;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°.其中能说明a∥b的条件有( )个.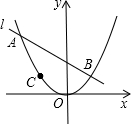 如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.
如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.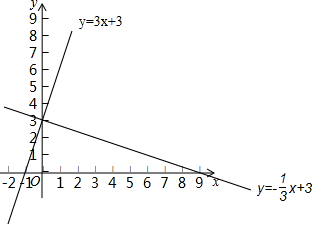 如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.
如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.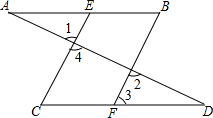 如图,已知AD与AB,CD相交于A,D两点,EC,BF与AB,CD相交于点E,C,B,F,且∠1=∠2,∠B=∠C,
如图,已知AD与AB,CD相交于A,D两点,EC,BF与AB,CD相交于点E,C,B,F,且∠1=∠2,∠B=∠C,