题目内容
“国美商场”销售某品牌汤锅,其成本为每件80元,9月份的销售额为2万元,10月份商场对这种汤锅的售价打9折销售,结果销售量增加了50件,销售额增加了0.7万元.(销售额=销售量×售价)
(1)求“国美商场”9月份销售该品牌汤锅的销售单价;
(2)11月11日“购物节”商场在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=﹣50x+600.问商场打几折时利润最大,最大利润是多少?
(3)在(2)的条件下,为保证“国美商场”利润不低于1.5万元,且能够最大限度帮助厂家减少库存,“国美”商场应该在9月份销售价的基础上打几折?
【考点】二次函数的应用;分式方程的应用;一元一次不等式的应用.
【分析】(1)根据人民商场销售某保温水瓶,其成本为每件80元,9月份的销售额为2万元,10月份商场对这种保温瓶的售价打9折销售,结果销售量增加了50件,销售额增加了0.7万元,可以设出9月份的保温瓶销售单价和销售数量,从而可以列出相应的二元一次方程组,即可解答本题;
(2)根据题意可以列出销售利润的关系式,将其化为顶点式,即可求得最大利润和此时的打折数;
(3)由(2)和题意可以列出相应的关系式,从而可以求得x的范围,结合题意取舍即可.
【解答】解:(1)设9月份销售价格为每件x元,据题意可得:
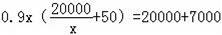
 ,
,
解得:x=200.
答:9月份每件销售200元.
(2)设国美商场在11月11日购物节销售该品牌的利润为L元,
则:L=200×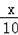
 (﹣50x+600)﹣80(﹣50x+600)(x≥4),
(﹣50x+600)﹣80(﹣50x+600)(x≥4),
L=﹣1000×x2+16000x﹣48000=﹣1000(x﹣8)2+16000,
当x=8时,最大利润为16000元.
答:商场打8折时利润最大,最大利润是16000元;
(3)200×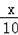
 (﹣50x+600)﹣80(﹣50x+600)≥15000,
(﹣50x+600)﹣80(﹣50x+600)≥15000,
解得7≤x≤9.
当7≤x≤9时,函数y=﹣50x+600的值随着x的增大而减小,
因此当x=7时,利润不低于15000元,且又能够最大限度减少厂家库存.
【点评】本题考查二次函数的应用,解题的关键是明确题意,能根据题目的要求,列出相应的表达式,会求函数的最值.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
 B.
B.


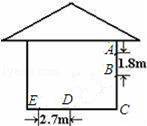


 的图象经过点(2,6),那么k的值为( )
的图象经过点(2,6),那么k的值为( )
 =0的两根,若实数a满足a+x1+x2﹣x1•x2=2018,则a= .
=0的两根,若实数a满足a+x1+x2﹣x1•x2=2018,则a= .
 |+(
|+(
 )﹣1﹣(1+
)﹣1﹣(1+
 )0+2•tan60°
)0+2•tan60°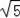
 ,OP=1,求BC的长.
,OP=1,求BC的长.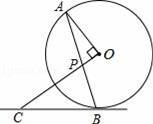

 是二元一次方程
是二元一次方程 的解,则
的解,则 的值是________.
的值是________.