题目内容
17. 二次函数y=2$\sqrt{3}$x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
二次函数y=2$\sqrt{3}$x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
分析 连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=$\sqrt{3}$BD,设BD=t,则OD=$\sqrt{3}$t,B(t,$\sqrt{3}$t),利用二次函数图象上点的坐标特征得2$\sqrt{3}$t2=$\sqrt{3}$t,得出BD=$\frac{1}{2}$,OD=$\frac{\sqrt{3}}{2}$,然后根据菱形的性质得出C点坐标.
解答 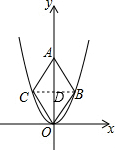 解:连结BC交OA于D,如图,
解:连结BC交OA于D,如图,
∵四边形OBAC为菱形,
∴BC⊥OA,
∵∠OBA=120°,
∴∠OBD=60°,
∴OD=$\sqrt{3}$BD,
设BD=t,则OD=$\sqrt{3}$t,
∴B(t,$\sqrt{3}$t),
把B(t,$\sqrt{3}$t)代入y=2$\sqrt{3}$x2得2$\sqrt{3}$t2=$\sqrt{3}$t,解得t1=0(舍去),t2=$\frac{1}{2}$,
∴BD=$\frac{1}{2}$,OD=$\frac{\sqrt{3}}{2}$,
故C点坐标为:(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了菱形的性质、二次函数图象上点的坐标特征,根据二次函数图象上点的坐标性质得出BD的长是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5. 在小孔成像问题中,光线穿过小孔,在屏幕上形成倒立的实像,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是AB长的( )
在小孔成像问题中,光线穿过小孔,在屏幕上形成倒立的实像,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是AB长的( )
 在小孔成像问题中,光线穿过小孔,在屏幕上形成倒立的实像,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是AB长的( )
在小孔成像问题中,光线穿过小孔,在屏幕上形成倒立的实像,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是AB长的( )| A. | 3倍 | B. | $\frac{1}{2}$ | ||
| C. | $\frac{1}{3}$ | D. | 不知AB的长度,无法判断 |
12.为了了解某校八年级1000名学生的身高情況,从中抽查了100名学生的身高进行统计分析,在这个问题中,总体是指( )
| A. | 1000名学生 | B. | 被抽取的100名学生 | ||
| C. | 1000名学生的身高 | D. | 被抽取的100名学生的身高 |
6.若多项式3x2-2xy-y2减去多项式M所得的差是-5x2+xy-2y2,则多项式M是( )
| A. | -2x2-xy-3y2 | B. | 2x2+xy+3y2 | C. | 8x2-3xy+y2 | D. | -8x2+3xy-y2 |
7.若一个三角形各边的长度都扩大2倍,则扩大后的三角形各角的度数都( )
| A. | 缩小2倍 | B. | 不变 | C. | 扩大2倍 | D. | 扩大4倍 |
 如图,在△ABC与△ABD中,AD与BC相交于点O.∠1=∠2,请你添加一个条件(不再添加其他线段相等,不标注或使用其他字母),使OC=OD,并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于点O.∠1=∠2,请你添加一个条件(不再添加其他线段相等,不标注或使用其他字母),使OC=OD,并给出证明. 现有甲、乙两支同样的温度计,将它们按如图位置放置,如果向左移动甲温度计,使其度数12与乙温度计的度数-6对齐,那么此时乙温度计与甲温度计数-4对齐的度数是10.
现有甲、乙两支同样的温度计,将它们按如图位置放置,如果向左移动甲温度计,使其度数12与乙温度计的度数-6对齐,那么此时乙温度计与甲温度计数-4对齐的度数是10.