题目内容
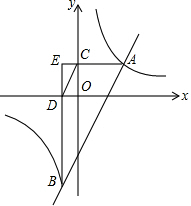 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
(1)求证:AB∥CD;
(2)若a=2,△ABE的面积为9,求反比例函数的解析式;
(3)在(2)的条件下,连接OB,P为双曲线上一点,以OB、OP为邻边作平行四边形,且平行四边形的周长最小,求第四个顶点Q的坐标.
考点:反比例函数综合题
专题:
分析:(1)设A(x1,
),B(x2,
),根据题意可得AE=x1-x2,BE=
-
,EC=-x2,ED=
,然后求得
=
=-
,即可求得.
(2)先求得直线与x轴、y轴的交点,然后根据AE∥OM,BE∥ON,∠E=∠MON=90°,求得△ABE∽△MNO,根据相似三角形的性质得出
=
=
,根据三角形的面积结合交点和系数的关系即可求得.
(3)因为四边形OBPQ是平行四边形,所以OB=PQ,OP=BQ,而点B是定点,所以OB的长也是定长,所以要求平行四边形OBPQ周长的最小值就只需求OP的最小值,结合勾股定理求得P的坐标,进而求得Q的坐标.
| k |
| x1 |
| k |
| x2 |
| k |
| x1 |
| k |
| x2 |
| k |
| x1 |
| AE |
| BE |
| EC |
| ED |
| x1x2 |
| k |
(2)先求得直线与x轴、y轴的交点,然后根据AE∥OM,BE∥ON,∠E=∠MON=90°,求得△ABE∽△MNO,根据相似三角形的性质得出
| AE |
| BE |
| OM |
| ON |
| 1 |
| 2 |
(3)因为四边形OBPQ是平行四边形,所以OB=PQ,OP=BQ,而点B是定点,所以OB的长也是定长,所以要求平行四边形OBPQ周长的最小值就只需求OP的最小值,结合勾股定理求得P的坐标,进而求得Q的坐标.
解答:解:(1)设A(x1,
),B(x2,
),
根据题意AE=x1-x2,BE=
-
,EC=-x2,ED=
,
∵
=
=-
,
=
=-
,
∴
=
,
∴
=
,
∴AB∥CD;
(2)∵a=2,
∴一次函数为y=2x-2,
∴直线y=2x-2交x轴M的坐标为(1,0),交y轴N的坐标为(0,-2),
∴OM=1,ON=2,
∵AC⊥y轴于点C,BD⊥x轴于点D.
∴AE∥OM,BE∥ON,∠E=∠MON=90°,
∴△ABE∽△MNO,
∴
=
=
,
∴BE=2AE,
∵AE=x1-x2,
∴BE=2(x1-x2),
由
得,x2-x-
=0,
∴x1+x2=1,x1x2=-
,
∵SABE=
AE•BE=
(x1-x2)•2(x1-x2)=(x1-x2)2=(x1+x2)2-4x1x2=1-4×(-
)=1+2k=9,
∴k=4,
∴反比例函数的解析式为y=
;
(3)由
可知B的坐标为(-1,-4),
因为四边形OBPQ是平行四边形,所以OB=PQ,OP=BQ,
而点B是定点,所以OB的长也是定长,
所以要求平行四边形OBPQ周长的最小值就只需求OP的最小值,
因为点P在双曲线上,所以可设点P的坐标为(n,
),
由勾股定理可得OP2=n2+
=n2+
-8+8=(n-
)2+8,
所以当(n-
)2=0即n-
=0时,OP2有最小值,OP有最小值,
解得,n=±2,
∴P(2,2)或(-2,-2),
∴Q(1,-2)或(-3,-6);
| k |
| x1 |
| k |
| x2 |
根据题意AE=x1-x2,BE=
| k |
| x1 |
| k |
| x2 |
| k |
| x1 |
∵
| AE |
| BE |
| x1-x2 | ||||
|
| x1x2 |
| k |
| EC |
| ED |
| -x2 | ||
|
| x1x2 |
| k |
∴
| AE |
| BE |
| EC |
| ED |
∴
| EC |
| AE |
| ED |
| BE |
∴AB∥CD;
(2)∵a=2,
∴一次函数为y=2x-2,
∴直线y=2x-2交x轴M的坐标为(1,0),交y轴N的坐标为(0,-2),
∴OM=1,ON=2,
∵AC⊥y轴于点C,BD⊥x轴于点D.
∴AE∥OM,BE∥ON,∠E=∠MON=90°,
∴△ABE∽△MNO,
∴
| AE |
| BE |
| OM |
| ON |
| 1 |
| 2 |
∴BE=2AE,
∵AE=x1-x2,
∴BE=2(x1-x2),
由
|
| k |
| 2 |
∴x1+x2=1,x1x2=-
| k |
| 2 |
∵SABE=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
∴k=4,
∴反比例函数的解析式为y=
| 4 |
| x |
(3)由
|
因为四边形OBPQ是平行四边形,所以OB=PQ,OP=BQ,
而点B是定点,所以OB的长也是定长,
所以要求平行四边形OBPQ周长的最小值就只需求OP的最小值,
因为点P在双曲线上,所以可设点P的坐标为(n,
| 4 |
| n |
由勾股定理可得OP2=n2+
| 16 |
| n2 |
| 16 |
| n2 |
| 4 |
| n |
所以当(n-
| 4 |
| n |
| 4 |
| n |
解得,n=±2,
∴P(2,2)或(-2,-2),
∴Q(1,-2)或(-3,-6);
点评:此题考查了反比例综合题,涉及的知识有:坐标与图形性质,相似三角形的判定和性质,平行四边形的判定与性质,待定系数法确定函数解析式,以及三角形的面积求法.

练习册系列答案
相关题目
解方程6(1-
)=1,去括号得( )
| 1-x |
| 3 |
| A、6-2+2x=6 | ||
| B、6-2+2x=1 | ||
C、6-
| ||
| D、6-2-x=1 |
已知代数式y2-2y+6的值为8,那么代数式2y2-4y+1的值为( )
| A、2 | B、3 | C、4 | D、5 |
 已知a、b、c在数轴上的位置如图所示,试求|a|+|c-3|+|b|的值.
已知a、b、c在数轴上的位置如图所示,试求|a|+|c-3|+|b|的值. 如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元. 观察月历:
观察月历: