Question

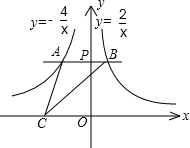如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数 y=-

4

x

和y=

2

x

y=-

4

x

和y=

2

x

的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（　　）

• A、3
• B、4
• C、5
• D、6

Answer 1

考点：反比例函数系数k的几何意义

专题：计算题

分析：连接OA、OB，如图，由于AB∥x轴，根据反比例函数k的几何意义得到S_△OAP=2，S_△OBP=1，则S_△OAB=3，然后利用AB∥OC，根据三角形面积公式即可得到S_△CAB=S_△OAB=3．

解答：解：连接OA、OB，如图，
∵AB∥x轴，
∴S_△OAP=

1

2

×|-4|=2，S_△OBP=

1

2

×|2|=1，
∴S_△OAB=3，
∵AB∥OC，
∴S_△CAB=S_△OAB=3．
故选A．

点评：本题考查了反比例函数y=

k

x

（k≠0）系数k的几何意义：从反比例函数y=

k

x

（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．