题目内容
一元二次方程x2+5x+7=0解的情况是（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
考点：根的判别式
专题：计算题
分析：先计算判别式的值，然后根据判别式的意义判断根的情况．
解答：解：∵△=52-4×7=-3＜0，
∴方程没有实数根．
故选C．
∴方程没有实数根．
故选C．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
某宾馆在重新装修后，准备在新大厅的楼梯上铺设某种红色地毯，已知这种地毯每平方米售价30元，楼梯宽2米，其侧面如图，则购买地毯至少需要
已知二次函数y=ax2+bx+c（a≠0）的图象如图，并且图象经过点（1，0）、（0，2），对称轴为x=-| 1 |
| 4 |
①abc＜0；②4ac-b2＞0；③a-b+c＞2；④a＜b＜0；⑤ac+2=b．
其中正确的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
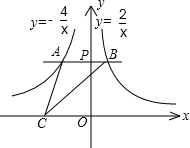如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数 y=-| 4 |
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| A、3 | B、4 | C、5 | D、6 |
在0、-1，1，-0.1，2，-3这六个数中，最小的数是（ ）
| A、0 | B、-0.1 | C、-1 | D、-3 |
已知A（3，-4）将A点向左平移1个单位，再向下平移2个单位得到B点，则B点关于x轴的对称点B′坐标是（ ）
| A、（2，-6） |
| B、（-2，-6） |
| C、（-2，6） |
| D、（2，6） |
如图，下列图案是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
实数a、b在数轴上对应的点分别在原点的左边和右边，则
-
=（ ）
| -a3b |
| -ab3 |
A、（a+b）
| ||
B、（-a+b）
| ||
C、（a-b）
| ||
D、（-a-b）
|
某班为奖励在校运会上取得较好成绩的运动员，花了400元钱购买甲、乙两种奖品共30件，其中甲种奖品每件6元，乙种奖品每件12元，求甲乙两种奖品各买多少件？该问题中，若设购买甲种奖品x件，乙种奖品y件，则方程组正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|