题目内容
9．一个三角形的面积是a2-ab-2b2，它的底是a+b，则它的高是（ ）| A． | $\frac{a}{2}$-b | B． | a-2b | C． | 2a+4b | D． | 2a-4b |
分析 先将a2-ab-2b2分解因式，然后利用三角形的面积公式可求得它的高．
解答 解：a2-ab-2b2=a2+ab-2ab-2b2
=a（a+b）-2b（a+b）
=（a-2b）（a+b）．
三角形的高=$\frac{2（a-2b）（a+b）}{a+b}$=2a-4b．
故选：D．
点评 本题主要考查的是整式的除法，将a2-ab-2b2分解为（a-2b）（a+b）是解题的关键．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
如图．在直角三角形BCD中，∠D=90°∠DBC=15°，点A在直角边BD上，连接AC，AB=AC=4．求CD的长．
14．多项式-6y4+5x2y3-4x3+ax4y3是（ ）
| A． | 按字母π的降幂排列的 | B． | 按字母y的升幂排列的 | ||
| C． | 按字母x的升幂排列的 | D． | 按字母y的降幂排列的 |
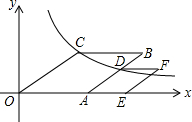如图，在菱形OABC中，点A落在x轴正半轴，反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象经过点C，与AB交于点D，以AD为一边向右作菱形AEFD，点E落在x轴上．已知∠AOC=30°，OA•AE=12，则菱形OABC的面积与菱形AEFD的面积差是4$\sqrt{3}$．