题目内容

19．已知关于x的一元二次方程x2+mx-2=0
（1）若x=-1是这个方程的一个根，求m的值；
（2）对于任意的实数m，判断方程的根的情况，并说明理由．

分析 （1）把x=-1代入方程求出m的值即可；
（2）表示出根的判别式，由根的判别式的值恒大于0，即可确定出方程根的情况．

解答 解：（1）将x=-1代入方程x2-mx-2=0，得1+m-2=0，
解得：m=1；
（2）∵△=m2+8＞0，
∴对于任意的实数m，方程有两个不相等的实数根．

点评 此题考查了根的判别式，以及一元二次方程的解，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
9．计算：
（1）（$\sqrt{3}+\sqrt{2}$）-1+$\sqrt{（-2）^{2}}$+$\root{3}{-8}$
（2）4$\sqrt{5}$+$\sqrt{45}$$-\sqrt{8}+4\sqrt{2}$
（3）（1+$\sqrt{2}$-$\sqrt{3}$）（1-$\sqrt{2}$+$\sqrt{3}$）-2$\sqrt{6}$
（4）$\sqrt{50}$-（$\sqrt{8}$+2$\sqrt{\frac{1}{2}}$）+$\sqrt{（\sqrt{2}-3）^{2}}$．
10．求值：（-3）3÷2$\frac{1}{4}$×（-$\frac{2}{3}$）2+4-22×（-$\frac{1}{3}$）+（-1）2012．
7．⊙O半径为4$\sqrt{3}$cm，△ABC内接于⊙O，BC=12cm，则∠A=60°或120°．
14．计算：$\sqrt{4}+（-1{）^{2015}}+（π-3.14{）^0}$．
4．对于抛物线y=-$\frac{1}{3}$（x-5）2+3，下列说法正确的是（　　）
A．开口向上B．顶点坐标（-5，3）
C．与y轴的交点坐标是（0，3）D．当x＞5时，y随x的增大而减小
11．计算下列各式结果等于x4的是（　　）
A．x2+x2B．x2•x2C．x3+xD．x4•x
8．设同一个圆的内接正六边形、正八边形、正十二边形的边心距分别为r6，r8，r12，则r6，r8，r12的大小关系为（　　）
A．r6＞r8＞r12B．r6＜r8＜r12C．r8＞r6＞r12D．不能确定
9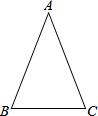．如图，△ABC中，AB=AC=13cm，BC=10cm．则△ABC内切圆的半径是（　　）
A．$\frac{10}{3}$B．$\frac{13}{2}$C．4D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网