题目内容
7.⊙O半径为4$\sqrt{3}$cm,△ABC内接于⊙O,BC=12cm,则∠A=60°或120°.分析 连接OB、OC,作OD⊥BC于D,则∠ODB=90°,由垂径定理得出BD=CD=BC=6cm,由等腰三角形的性质得出∠BOD=∠COD=$\frac{1}{2}$∠BOC,由三角函数求出∠BOD=60°,得出∠BOC=120°,分两种情况讨论,由圆周角定理即可得出结果.
解答 解:分两种情况: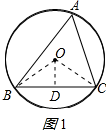
①当△ABC是锐角三角形时;
连接OB、OC,作OD⊥BC于D,如图1所示:
则∠ODB=90°,BD=CD=$\frac{1}{2}$BC=6cm,∠BOD=∠COD=$\frac{1}{2}$∠BOC,
∵sin∠BOD=$\frac{BD}{OB}$=$\frac{\sqrt{3}}{2}$,∴∠BOD=60°,
∴∠BOC=120°,
∴∠A=$\frac{1}{2}$∠BOC=60°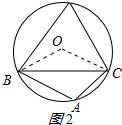
②当△ABC是钝角三角形时,如图2所示:
∠A=180°-60°=120°;
综上所述:∠A的度数为60°或120°;
故答案为:60°或120°.
点评 本题考查了三角形的外接圆、垂径定理、等腰三角形的性质、圆周角定理、三角函数等知识;本题综合性强,难度适中,求出∠BOC是解决问题的关键,注意分类讨论.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
18.已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
12.下列数中不是不等式2x-1>0的解的是( )
| A. | 1 | B. | 0 | C. | 2 | D. | 3 |