题目内容
9.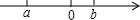 如图,已知实数a,b在数轴上位置如图所示,试化简$\sqrt{{(a-b)}^{2}}$+$\sqrt{{b}^{2}}$-|a+b|.
如图,已知实数a,b在数轴上位置如图所示,试化简$\sqrt{{(a-b)}^{2}}$+$\sqrt{{b}^{2}}$-|a+b|.
分析 首先根据实数a、b数轴上位置判断出a-b,b以及a+b的正负,然后利用$\sqrt{{a}^{2}}$=|a|进行化简,最后再化简绝对值,合并同类项即可.
解答 解:由实数a,b在数轴上位置可知:a-b<0,b>0,a+b<0
原式=|a-b|+|b|-|a+b|
=b-a+b+a+b
=3b.
点评 本题主要考查的是二次根式的性质,根据实数a,b在数轴上位置确定出a-b<0,b>0,a+b<0是解题的关键.

练习册系列答案
相关题目
1.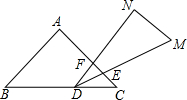 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )| A. | 105° | B. | 115° | C. | 120° | D. | 135° |
 十字交叉线
十字交叉线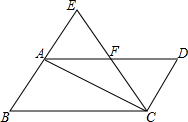 如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )