题目内容
 已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积.请直接写出点P的坐标
已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积.请直接写出点P的坐标考点:坐标与图形性质,三角形的面积
专题:
分析:利用△PAD的面积等于△POC的面积,得出EO的长,进而得出PE的长,即可得出P点坐标.
解答: 解:如图,过点P作PE⊥y轴于点E.
解:如图,过点P作PE⊥y轴于点E.
因为△PAD的面积等于△POC的面积,
所以3AE=5OE,即3(8-OE)=5OE,
解得:OE=3
所以△PAD的面积=△POC的面积=
×3×5=7.5,
△PAO的面积=△PCD的面积=[﹙3﹢5﹚×8÷2-2×7.5]÷2=8.5,
则
×8PE=8.5,即PE=
,
所以点P的坐标是(
,3).
故答案为:(
,3).
 解:如图,过点P作PE⊥y轴于点E.
解:如图,过点P作PE⊥y轴于点E.因为△PAD的面积等于△POC的面积,
所以3AE=5OE,即3(8-OE)=5OE,
解得:OE=3
所以△PAD的面积=△POC的面积=
| 1 |
| 2 |
△PAO的面积=△PCD的面积=[﹙3﹢5﹚×8÷2-2×7.5]÷2=8.5,
则
| 1 |
| 2 |
| 17 |
| 8 |
所以点P的坐标是(
| 17 |
| 8 |
故答案为:(
| 17 |
| 8 |
点评:此题主要考查了坐标与图形的性质以及三角形面积,利用三角形面积关系得出EO,PE的长是解题关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
如果|a-1|=0,(b+3)2=0,那么
+1的值是( )
| b |
| a |
| A、-2 | B、-3 | C、-4 | D、4 |
 一个扇形,如图,它的半径为30cm,圆心角为150°.用它做成一个圆锥的侧面,求所围成得圆锥的底面积的大小.
一个扇形,如图,它的半径为30cm,圆心角为150°.用它做成一个圆锥的侧面,求所围成得圆锥的底面积的大小.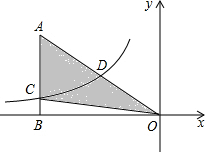 如图,已知反比例函数y=
如图,已知反比例函数y=