题目内容
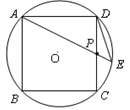
 如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
 解:如图,设圆心为O,连接OD、OE,过点O作OF⊥DE于F,
解:如图,设圆心为O,连接OD、OE,过点O作OF⊥DE于F,由圆周角定理得,∠DAF=
 ∠DOE,
∠DOE,由垂径定理可得,∠DOF=
 ∠DOE,DE=2DF,
∠DOE,DE=2DF,又∵∠ADC=∠OFD=90°,
∴△ADP∽△OFD,
∴
 =
= ,
,∵正方形ABCD的边长为1,
∴OD=
 ×
× =
= ,
,∵P是CD的中点,
∴DP=
 ,
,根据勾股定理,AP=
 =
= ,
,∴
 =
= ,
,解得DF=
 ,
,∴DE=2DF=2×
 =
= .
.分析:设圆心为O,连接OD、OE,过点O作OF⊥DE于F,根据圆周角定理可得∠DAF=
 ∠DOE,根据垂径定理可得∠DOF=
∠DOE,根据垂径定理可得∠DOF= ∠DOE,DE=2DF,然后求出△ADP和△OFD相似,根据相似三角形对应边成比例可得
∠DOE,DE=2DF,然后求出△ADP和△OFD相似,根据相似三角形对应边成比例可得 =
= ,再根据正方形的性质求出OD,利用勾股定理列式求出AP,然后代入比例式进行计算即可求出DF,然后求出DE.
,再根据正方形的性质求出OD,利用勾股定理列式求出AP,然后代入比例式进行计算即可求出DF,然后求出DE.点评:本题考查了相似三角形的判定与性质,圆周角定理,垂径定理,正方形的性质,作辅助线构造出直角三角形与相似三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
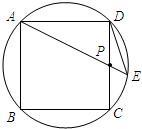 如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.
如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.
 E作
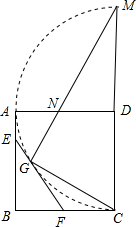
E作 如图,已知正方形边长为4,以A为圆心,AB为半径作
如图,已知正方形边长为4,以A为圆心,AB为半径作 如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.