题目内容
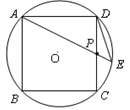
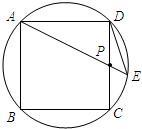 如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.
如图,已知:边长为1的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.(1)求弦DE的长.
(2)若Q是线段BC上一动点,当BQ长为何值时,三角形ADP与以Q,C,P为顶点的三角形相似?
分析:(1)过D点作DF⊥AE于F点.则△DEF是等腰直角三角形,根据△ADP的面积就可以求出DF,则根据勾股定理得到DE.
(2)△ADP与以Q,C,P为顶点的三角形相似,应分Rt△ADP∽Rt△PCQ和Rt△ADP∽Rt△PCQ两种情况进行讨论.根据相似三角形的对应边的比相等,得到BQ的长.
(2)△ADP与以Q,C,P为顶点的三角形相似,应分Rt△ADP∽Rt△PCQ和Rt△ADP∽Rt△PCQ两种情况进行讨论.根据相似三角形的对应边的比相等,得到BQ的长.
解答:解:(1)如图1.过D点作DF⊥AE于F点.
在Rt△ADP中,AP=
=
(1分)
又∵S△ADP=
AD•DP=
AP•DF
∴DF=
(2分)
∵
的度数为90°
∴∠DEA=45°
∴DE=
DF=
(4分)

(2)如图2.
当Rt△ADP∽Rt△QCP时有
=
得:QC=1.
即点Q与点B重合
∴BQ=0(5分)
如图3,当Rt△ADP∽Rt△PCQ时,有
=
得QC=
即BQ=BC-CQ=
(7分)
∴当BQ=0或BQ=
时,三角形ADP与以点Q,C,P为顶点的三角形相似.(8分)
在Rt△ADP中,AP=
| AD2+DP2 |
| ||
| 2 |
又∵S△ADP=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| ||
| 5 |
∵
 |
| AD |
∴∠DEA=45°
∴DE=
| 2 |
| ||
| 5 |

(2)如图2.
当Rt△ADP∽Rt△QCP时有
| AD |
| QC |
| DP |
| CP |
即点Q与点B重合
∴BQ=0(5分)
如图3,当Rt△ADP∽Rt△PCQ时,有
| AD |
| PC |
| PD |
| QC |
| 1 |
| 4 |
即BQ=BC-CQ=
| 3 |
| 4 |
∴当BQ=0或BQ=
| 3 |
| 4 |
点评:此题主要考查相似三角形的判定方法,勾股定理及正多边形与圆的关系等知识点的综合运用.

练习册系列答案
相关题目
 E作
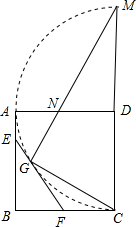
E作 如图,已知正方形边长为4,以A为圆心,AB为半径作
如图,已知正方形边长为4,以A为圆心,AB为半径作 如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.