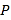ЬтФПФкШн
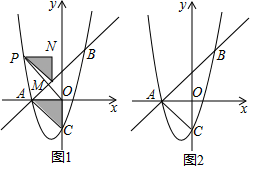
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпyЃН![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉжБЯпyЃНЉxЉ2гыИУХзЮяЯпдкЕкЫФЯѓЯоФкНЛгкЕуDЃЌгыxжсНЛгкЕуFЃЌСЌНгACЃЌCDЃЌЯпЖЮACгыЯпЖЮDFНЛгкЕуGЃЌЧѓжЄЃКЁїAGFЁеЁїCGDЃЛ
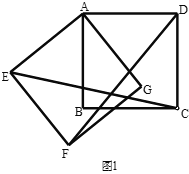
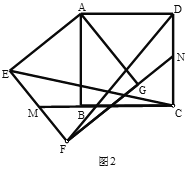
ЃЈ3ЃЉжБЯпyЃНmЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЈЕуMдкЕуNЕФзѓВрЃЉЃЌЕуMЙигкyжсЕФЖдГЦЕуЮЊЕуMЁфЃЌЕуHЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌШєЫФБпаЮNHOMЁфЕФУцЛ§ЮЊ![]() ЃЌЧѓЕуHЕНOMЁфЕФОрРыdЃЎ
ЃЌЧѓЕуHЕНOMЁфЕФОрРыdЃЎ
ЁОД№АИЁП(1) yЃН![]() x2Љ
x2Љ![]() xЉ3,C(0,-3);(2)МћНтЮі;(3)
xЉ3,C(0,-3);(2)МћНтЮі;(3) ![]()
ЁОНтЮіЁП
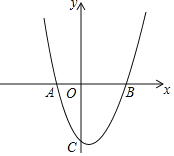
ЃЈ1ЃЉИљОнХзЮяЯпyЃН![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌПЩЕУХзЮяЯпЕФНтЮіЪНЃЛ
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌПЩЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнFЃЈ-2ЃЌ0ЃЉЃЌAЃЈ-1ЃЌ0ЃЉЃЌПЩЕУAF=1ЃЌдйИљОнЕуDЕФзјБъЮЊЃЈ1ЃЌ-3ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌ-3ЃЉЃЌПЩЕУCDЁЮxжсЃЌCD=1ЃЌдйИљОнЁЯAFG=ЁЯCDGЃЌЁЯFAG=ЁЯDCGЃЌМДПЩХаЖЈЁїAGFЁеЁїCGDЃЛ
ЃЈ3ЃЉИљОнжсЖдГЦЕФаджЪЕУГіOH=1=M'NЃЌНјЖјХаЖЈЫФБпаЮOM'NHЪЧЦНааЫФБпаЮЃЌдйИљОнЫФБпаЮOM'NHЕФУцЛ§ЮЊ![]() ЃЌЧѓЕУOP=
ЃЌЧѓЕУOP=![]() ЃЌдйИљОнЕуMЕФзјБъЮЊЃЈ
ЃЌдйИљОнЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЕУЕНPM'ЃН
ЃЉЃЌЕУЕНPM'ЃН![]() RtЁїOPM'жаЃЌдЫгУЙДЙЩЖЈРэПЩЕУOM'=
RtЁїOPM'жаЃЌдЫгУЙДЙЩЖЈРэПЩЕУOM'=![]() ЃЌзюКѓИљОнOM'ЁСd=
ЃЌзюКѓИљОнOM'ЁСd=![]() ЃЌМДПЩЕУЕНd=
ЃЌМДПЩЕУЕНd=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃН![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌ
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌ
Ёр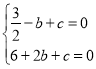 ЃЌ
ЃЌ
НтЕУ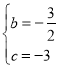 ЃЌ
ЃЌ
ЁрИУХзЮяЯпЕФНтЮіЪНyЃН![]() x2Љ
x2Љ![]() xЉ3ЃЎ
xЉ3ЃЎ
СюxЃН0ЃЌдђyЃНЉ3ЃЌ
ЁрCЃЈ0ЃЌЉ3ЃЉЃЛ
ЃЈ2ЃЉжЄУїЃКЁпжБЯпEFЕФНтЮіЪНЮЊyЃНЉxЉ2ЃЌ
ЁрЕБyЃН0ЪБЃЌxЃНЉ2ЃЌ
ЁрFЃЈЉ2ЃЌ0ЃЉЃЌOFЃН2ЃЌ
ЁпAЃЈЉ1ЃЌ0ЃЉЃЌ
ЁрOAЃН1ЃЌ
ЁрAFЃН2Љ1ЃН1ЃЌ
гЩ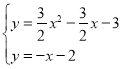 НтЕУ
НтЕУ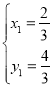 ЃЌ
ЃЌ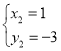 ЃЌ
ЃЌ
ЁпЕуDдкЕкЫФЯѓЯоЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ1ЃЌЉ3ЃЉЃЌ
ЁпЕуCЕФзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЌ
ЁрCDЁЮxжсЃЌCDЃН1ЃЌ
ЁрЁЯAFGЃНЁЯCDGЃЌЁЯFAGЃНЁЯDCGЃЌ
дкЁїAGFгыЁїCGDжа

ЁрЁїAGFЁеЁїCGDЃЈASAЃЉЃЛ
ЃЈ3ЃЉЁпХзЮяЯпЕФЖдГЦжсЮЊxЃНЉ![]() ЃН
ЃН![]() ЃЌжБЯпyЃНmЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЌ
ЃЌжБЯпyЃНmЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЌ
ЁрЕуMЁЂNЙигкжБЯпxЃН![]() ЖдГЦЃЌ
ЖдГЦЃЌ
ЩшNЃЈtЃЌmЃЉЃЌдђMЃЈ1ЉtЃЌmЃЉЃЌ
ЁпЕу MЙигкyжсЕФЖдГЦЕуЮЊЕуM'ЃЌ
ЁрM'ЃЈtЉ1ЃЌmЃЉЃЌ
ЁрЕуM'дкжБЯпyЃНmЩЯЃЌ
ЁрM'NЁЮxжсЃЌ
ЁрM'NЃНtЉЃЈtЉ1ЃЉЃН1ЃЌ
ЁпHЃЈ1ЃЌ0ЃЉЃЌ
ЁрOHЃН1ЃНM'NЃЌ
ЁрЫФБпаЮOM'NHЪЧЦНааЫФБпаЮЃЌ
ЩшжБЯпyЃНmгыyжсНЛгкЕуPЃЌ
ЁпЫФБпаЮOM'NHЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
ЁрOHЁСOPЃН1ЁСmЃН![]() ЃЌМДmЃН
ЃЌМДmЃН![]() ЃЌ
ЃЌ
ЁрOPЃН![]() ЃЌ
ЃЌ
ЕБ![]() x2Љ
x2Љ![]() xЉ3ЃН
xЉ3ЃН![]() ЪБЃЌ
ЪБЃЌ
НтЕУx1ЃНЉ![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЌ
ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрM'ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌМДPM'ЃН
ЃЉЃЌМДPM'ЃН![]() ЃЌ
ЃЌ
ЁрRtЁїOPM'жаЃЌOM'ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЫФБпаЮOM'NHЕФУцЛ§ЮЊ ![]() ЃЌ
ЃЌ
ЁрOM'ЁСdЃН![]() ЃЌ
ЃЌ
ЁрdЃН![]() ЃЎ
ЃЎ