Question

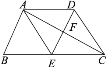
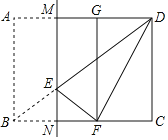
【题目】如图，在矩形ABCD中，AB：BC＝3：4，点E是对角线BD上一动点（不与点B，D重合），将矩形沿过点E的直线MN折叠，使得点A，B的对应点G，F分别在直线AD与BC上，当△DEF为直角三角形时，CN：BN的值为_____．

Answer 1

【答案】或．

【解析】

分两种情况进行讨论：当∠DFE＝90°时，△DEF为直角三角形；当∠EDF＝90°时，△DEF为直角三角形，分别判定△DCF∽△BCD，得到＝，进而得出CF，根据线段的和差关系可得CN和BN的长，于是得到结论．

解：∵AB：BC＝3：4，

设AB＝3x，BC＝4x，

∵四边形ABCD是矩形，

∴CD＝AB＝3x，AD＝BC＝4x，

分两种情况：

①如图所示，当∠DFE＝90°时，△DEF为直角三角形，

∵∠CDF+∠CFD＝∠EFN+∠CFD＝90°，

∴∠CDF＝∠EFN，

由折叠可得，EF＝EB，BN＝FN，

∴∠EFN＝∠EBN，

∴∠CDF＝∠CBD，

又∵∠DCF＝∠BCD＝90°，

∴△DCF∽△BCD，

∴＝，即＝，

∴CF＝，

∴FN＝NB＝＝，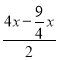

∴CN＝CF+NF＝+＝，

∴CN：BN＝：＝25：7．

②如图所示，当∠EDF＝90°时，△DEF为直角三角形，

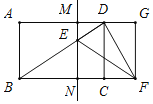
∵∠CDF+∠CDB＝∠CDF+∠CBD＝90°，

∴∠CDF＝∠CBD，

又∵∠DCF＝∠BCD＝90°，

∴△DCF∽△BCD，

∴＝，即＝，

∴CF＝，

∴NF＝BN＝＝，

∴CN＝NF﹣CF＝﹣＝，

∴CN：BN＝7：25，

综上所述，CN：BN的值为或．

故答案为：或．