题目内容
【题目】已知:正方形![]() 绕点
绕点![]() 顺时针旋转至正方形
顺时针旋转至正方形![]() ,连接
,连接![]() .
.
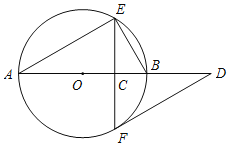
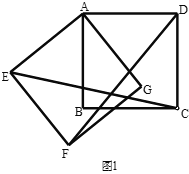
(1)如图,求证:![]() ;
;
(2)如图,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
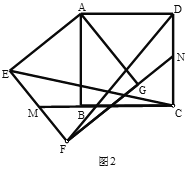
于![]() ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
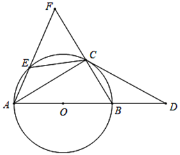
(1)连接AF、AC,易证∠EAC=∠DAF,再证明ΔEACΔDAF,根据全等三角形的性质即可得CE=DF;(2)由旋转的性质可得∠DAG、∠BAE都是旋转角,在四边形AEMB中,∠BAE+∠EMB=180°,∠FMC+∠EMB=180°,可得∠FMC=∠BAE,同理可得∠DAG=∠CNF,由此即可解答.
(1)证明:连接![]() ,
,

∵正方形![]() 旋转至正方形
旋转至正方形![]()
∴![]() ,
,![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
 ,
,
∴![]()
∴![]()
(2).∠DAG、∠BAE、∠FMC、∠CNF;
由旋转的性质可得∠DAG、∠BAE都是旋转角,在四边形AEMB中,∠BAE+∠EMB=180°,∠FMC+∠EMB=180°,可得∠FMC=∠BAE,同理可得∠DAG=∠CNF,

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目