题目内容
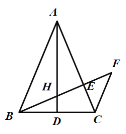
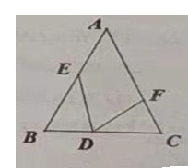
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上移动(点
边上移动(点![]() 不与
不与![]() 重合),满足
重合),满足![]() ,且点
,且点![]() 分别在
分别在![]() 上。
上。
(1)求证:![]() ∽
∽![]()
(2)当点![]() 移动到
移动到![]() 中点时,求证:点
中点时,求证:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上。
上。
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用等腰三角形性质得出∠B=∠C,之后利用等量代换得出∠BED=∠CDF从而证明三角形相似
(2)连接EF,由(1)得到△BDE∽△CFD,所以![]() ,进一步证明△DEF∽△CDF得出∠EFD=∠CFD从而证明结论
,进一步证明△DEF∽△CDF得出∠EFD=∠CFD从而证明结论
解(1)∵AB=AC
∴∠B=∠C
∵∠B=∠EDF
∴∠BED+∠BDE=∠BDE+∠CDF
∴∠BED=∠CDF
∴△BDE∽△CFD
(2)

如图,连接EF
∵△BDE∽△CFD
∴![]()
∵BD=CD
∴![]()
∵∠EDF=∠C
∴△DEF∽△CDF
∴∠EFD=∠CFD
∴E关于直线DF对称点在直线AC上

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目