题目内容
2．从长度分别为3，5，8，9的四条线段中随机抽取三条，能构成三角形的概率是$\frac{1}{2}$．分析 利用列举法就可以求出任意三条线段可以组成的组数．再根据三角形三边关系定理确定能构成三角形的组数，就可求出概率．
解答 解：这四条线段中任取三条，所有的结果有：
（3，5，8），（3，5，9），（5，8，9），（3，8，9）
共4个结果，
根据三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边，
其中能构成三角形的有（5，8，9），（3，8，9）两种情况，
故概率是$\frac{2}{4}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 考查了概率的求法及三角形的三边关系，注意分析任取三条的总情况，再分析构成三角形的情况，从而求出构成三角形的概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，将由线段组成的两边∠ACB沿O点旋转，使A点到D点．
10．cos45°的值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
17．
如图，已知∠AOB=60°，点P在边OA上，OP=10，点M，N在边OB上，PM=PN，若MN=2，则OM等于（ ）
如图，已知∠AOB=60°，点P在边OA上，OP=10，点M，N在边OB上，PM=PN，若MN=2，则OM等于（ ）| A． | 5$\sqrt{3}$ | B． | 5$\sqrt{3}$-1 | C． | 5 | D． | 4 |
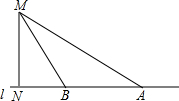如图，高速公路旁有一个测速站M到公路l的距离MN为60米，一辆小汽车在公路l上行驶，测得此车从点A行驶到点B所有的时间为3秒，已知∠MAN=30°，∠MBN=60°．