题目内容
10. 如图,AB是⊙0的直径,PQ是⊙0的切线,切点为C,求证:∠PCA=∠B.
如图,AB是⊙0的直径,PQ是⊙0的切线,切点为C,求证:∠PCA=∠B.
分析 连接OC,由切线的性质定理可知∠OCP=90°,再根据直径所对的边是直角可知∠ACB=90°,由同角的余角相等可知∠ACP=∠BCO,然后由∠B=∠OCB可证明∠PCA=∠B.
解答 证明:连接OC.
∵PQ是⊙O的切线,
∴∠OCP=∠OCA+∠ACP=90°.
∵AB是圆的直径,
∴∠ACB=90°.
∴∠ACO+∠OCB=90°.
∴∠ACP=∠OCB.
∵OC=OB,
∴∠OCB=∠B.
∴∠ACP=∠B.
点评 本题主要考查了圆的切线的性质定理,以及圆的直径所对的圆周角是直角掌握此类问题的辅助线的做法是解题的关键.

练习册系列答案
相关题目
5.设a=-(-3-2)2,b=(-3)×(-2),c=(-3)2÷(-2)2,则( )
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | c>a>b |
15.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
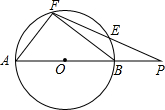 如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.
如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.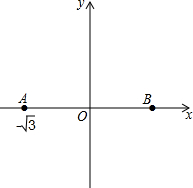 如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B
如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B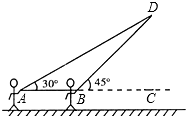 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).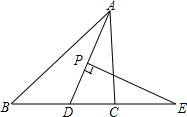 如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.