题目内容
10.不等式组$\left\{\begin{array}{l}3x+1<x-3\\ \frac{1+x}{2}≤\frac{1+2x}{3}+a\end{array}\right.$有且只有三个不同的整数解,则实数a的取值范围为1≤a<$\frac{7}{6}$.分析 先求出不等式组的解集,根据已知即可得出关于a的不等式组,求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{3x+1<x-3①}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+a②}\end{array}\right.$,
不等式①的解集是x<-2,
不等式②的解集是x≥1-6a,
∴不等式组的解集是1-6a≤x<-2,
∵关于x的不等式组有且只有三个整数解,
∴-6<1-6a≤-5,
解得:1≤a<$\frac{7}{6}$,
故答案为:1≤a<$\frac{7}{6}$.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,解此题的关键是能根据已知和不等式组的解集得出关于a的不等式组.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
20.平面内点A(-2,2)和点B(-2,6)的对称轴是( )
| A. | x轴 | B. | y轴 | C. | 直线y=4 | D. | 直线x=-2 |
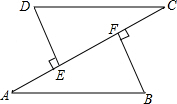 如图,AB=CD,AE=CF,DE⊥AC于E,BF⊥AC于F,求证:AB∥CD.
如图,AB=CD,AE=CF,DE⊥AC于E,BF⊥AC于F,求证:AB∥CD.