题目内容
12.探究:观察-$\frac{1}{2}$、$\frac{2}{3}$、-$\frac{3}{4}$、$\frac{4}{5}$、…,根据规律,第7个数是-$\frac{7}{8}$,第8个数是$\frac{8}{9}$,第2000个数是$\frac{2000}{2001}$.分析 分数的分子是从1开始连续的自然数,分母对应比分子大1,奇数位置为负,偶数位置为正,由此得出第n个数为(-1)n$\frac{n}{n+1}$,由此代入求得答案即可.
解答 解:∵第n个数为(-1)n$\frac{n}{n+1}$,
∴第7个数是-$\frac{7}{8}$,第8个数是$\frac{8}{9}$,第2000个数是$\frac{2000}{2001}$.
故答案为:-$\frac{7}{8}$,$\frac{8}{9}$,$\frac{2000}{2001}$.
点评 此题考查数字的变化规律,找出数字的运算规律和符号的变化规律是解决问题的关键.

练习册系列答案
相关题目
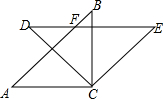 如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.
如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.