题目内容
2.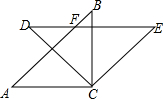 如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.
如图,在RT△ABC中,AC=BC,将△ABC绕点C顺时针旋转45°后得到△DEC,AB与DE相交于点F.(1)试判断DE与AC的位置关系并证明;
(2)试探究四边形ACEF是什么特殊的四边形,并证明你的结论;
(3)若AC=1,求BF的长.
分析 (1)由题意可知∠D=∠DCA=45°,从而可证明AD∥AC;
(2)由∠B=∠BCE=45°,从而可证明AB∥CE,从而可知四边形AFEC为平行四边形,然后由AC=CE,从而四边形ACEF是菱形;
(3)由菱形的性质可知AF=AC=1,然后由勾股定理可求得AB=$\sqrt{2}$,从而可求得BF的长.
解答 解:(1)∵在Rt△ABC中,AC=BC,
∴∠A=∠B=45°.
由旋转的性质可知:∠ACD=∠BCE=45°,∠D=∠A=45°.
∴∠D=∠DCA=45°.
∴DE∥AC.
(2)∵∠B=45°,∠BCE=45°,
∴∠B=∠BCE.
∴AB∥CE.
由(1)可知:DE∥AC,
∴四边形ACEF是平行四边形.
又∵AC=CE,
∴四边形ACEF是菱形.
(3)∵四边形ACEF是菱形,
∴AF=AC=1.
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
∴BF=AB-AF=$\sqrt{2}-1$.
点评 本题主要考查的是菱形的性质和判定、等腰直角三角形的性质、旋转的性质、勾股定理的应用,证得四边形ACEF是菱形是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
7.一个负数的绝对值是为2.9,则这个数是( )
| A. | 2.9 | B. | -2.9 | C. | -2.9或-5.8 | D. | -5.8 |
14.已知实数a、b、c满足$\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}$=k (注:a+b+c≠0),则直线y=kx-k不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
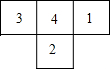 一个几何体由几个大小形状相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小立方块中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状.
一个几何体由几个大小形状相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小立方块中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状. 已知:如图,AC平分∠BAD,CE⊥AB与点E,CF⊥AD与点F,且BC=DC,你能说出BE与DF的数量关系吗?为什么?
已知:如图,AC平分∠BAD,CE⊥AB与点E,CF⊥AD与点F,且BC=DC,你能说出BE与DF的数量关系吗?为什么?