题目内容
4．连接任意四边形的四边中点得到的四边形是平行四边形．分析 连接对角线BD，根据三角形中位线的性质即可得出EN∥BD、EN=$\frac{1}{2}$BD，同理可得出FM∥BD、FM=$\frac{1}{2}$BD，由此得出EN∥FM、EN=FM，再根据平行四边形的判定定理即可得出四边形EFMN为平行四边形．
解答 解：连接对角线BD，如图所示．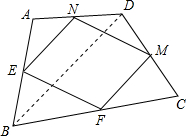
∵点E、N为AB、AD的中点，
∴EN为△ABD的中位线，
∴EN∥BD，且EN=$\frac{1}{2}$BD．
同理可得：FM∥BD，FM=$\frac{1}{2}$BD，
∴EN∥FM，EN=FM，
∴四边形EFMN为平行四边形．
故答案为：平行四边形．
点评 本题考查了中点四边形、三角形中位线定理以及平行四边形的判定定理，根据三角形中位线的性质得出EN∥FM、EN=FM是解题的关键．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
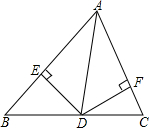如图，在△ABC中，∠BAC=60°，点D是BC边上一点，连接AD，过点D分别作DE⊥AB于E，DF⊥AC于F．若AD=10，且DE=DF，则DE的长为5．
如图，在⊙O中，点C在圆周上，∠ACB=45°，则∠AOB=90度．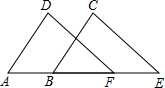
如图，AD=BC，FD=EC，再加上条件AF=BE，就可证∠D=∠C．