题目内容
11.已知点A是函数y=-$\frac{4}{x}$的图象上的一点,过A点作AM⊥x轴,垂足为M,连接OA,则△OAM的面积为2.分析 直接根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义求解.
解答 解:∵AM⊥x轴于点M,
∴△MAO的面积=$\frac{1}{2}$|k|=$\frac{1}{2}$×4=2.
故答案为:2.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
1.下列等式正确的是( )
| A. | 3-2=-9 | B. | -0.000000137=-1.37×107 | ||
| C. | (a2)-3=$\frac{1}{{a}^{6}}$ | D. | -$\frac{x-1}{x-y}$=$\frac{x+1}{x-y}$ |
6.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{8}$=3$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{4}$×$\sqrt{2}$=2 |
3.某商品进价10元,标价15元,为了促销,现决定打折销售,但每件利润不少于2元,则最多打几折销售( )
| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
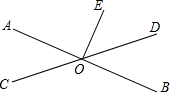 如图,直线AB,CD相交于点O,OE⊥AB于点O,∠COB=145°,则∠DOE=55°.
如图,直线AB,CD相交于点O,OE⊥AB于点O,∠COB=145°,则∠DOE=55°.