题目内容
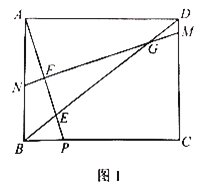
【题目】如图,在直角坐标系中,点B的坐标为![]() ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数
,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数![]() 的图象交AB,BC分别于点E,F.
的图象交AB,BC分别于点E,F.

(1)求直线EF的解析式.
(2)求四边形BEOF的面积.
(3)若点P在y轴上,且![]() 是等腰三角形,请直接写出点P的坐标.
是等腰三角形,请直接写出点P的坐标.
【答案】(1)![]() ;(2)1;(3)点P的坐标为
;(2)1;(3)点P的坐标为![]() 或
或![]() .
.
【解析】
(1)点E与点B的纵坐标相同,点F与点B的横坐标相同,分别将y=1,x=2代入反比例函数解析式,可求出E、F的坐标,然后采用待定系数法即可求出直线EF的解析式;
(2)利用![]() 即可求出答案;
即可求出答案;
(3)设P点坐标为(0,m),分别讨论OP=OE,OP=PE,OE=PE三种情况,利用两点间的距离公式求出m即可得到P点坐标.
解:(1)![]() 轴,
轴,![]() 轴,
轴,
将![]() 代入
代入![]() ,得
,得![]()
![]()
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]()
设直线EF的解析式为![]()
把E、F的坐标代入![]() 解得
解得
![]()
∴直线EF的解析式为![]()
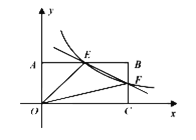
(2)由题意可得:
![]()
![]()
=1
(3)设P点坐标为(0,m),
∵E(1,1),
∴![]() ,
,![]() ,
,![]()
①当OP=OE时,![]() ,解得
,解得![]() ,
,![]()
∴P点坐标为![]() 或
或![]()
②当OP=PE时,![]() ,解得
,解得![]()
∴P点坐标为![]()
③当OE=PE时,![]() ,解得
,解得![]() ,
,![]()
当m=0时,P与原点重合,不符合题意,舍去,
∴P点坐标为![]()
综上所述,点P的坐标为![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目