题目内容
设n个正整数a1，a2，…，an，（其中n＞1），如果满足：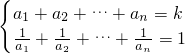
，则称k是一个“好数”．
如：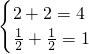
，
，
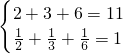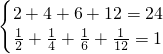，因此4、11、24这三个数都是一个好数．
（1）请你举一个“好数”的例子，并说明理由．
（2）如果k是“好数”，2k+2是“好数”吗？为什么？
解：（1）30为一个“好数”，理由为：
，
因此30为一个“好数”；
（2）如果k是“好数”，则有：，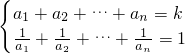
则2a1+2a2+…+2an+2=2k+2，
则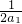
+
+…+
+
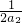=+=1，
故2k+2也是“好数”．
分析：（1）30为一个“好数”，理由为：2+3+10+15=30，且+
+
+
=1，根据题中的新定义得到30为一个“好数”；
（2）根据“好数”的定义得到2a1+2a2+…+2an+2=2k+2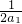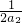，++…++=+=1，依此即可作出判断．
点评：本题主要考查“好数”的定义，解答本题的关键是掌握“好数”的定义的知识，本题（2）中得到2a1+2a2+…+2an+2=2k+2是本题的难点，此题难度较大．
，因此30为一个“好数”；
（2）如果k是“好数”，则有：
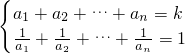，则2a1+2a2+…+2an+2=2k+2，
则
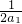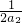++…++=+=1，故2k+2也是“好数”．
分析：（1）30为一个“好数”，理由为：2+3+10+15=30，且
+++=1，根据题中的新定义得到30为一个“好数”；（2）根据“好数”的定义得到2a1+2a2+…+2an+2=2k+2，
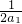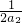++…++=+=1，依此即可作出判断．点评：本题主要考查“好数”的定义，解答本题的关键是掌握“好数”的定义的知识，本题（2）中得到2a1+2a2+…+2an+2=2k+2是本题的难点，此题难度较大．
练习册系列答案
智能训练练测考系列答案
相关题目