题目内容
如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB= ,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
(1)当圆C经过点A时,求CP的长;
(2)连结AP,当AP//CE时,求弦EF的长;
(3)当△AGE是等腰三角形时,求圆C的半径长.
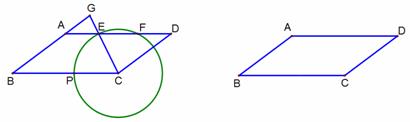
图1 备用图
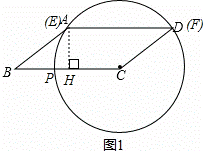 (1)如图1,设⊙O的半径为r,
(1)如图1,设⊙O的半径为r,
当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,
∴BH=AB 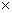 cosB=4,
cosB=4,
∴AH=3,CH=4,············1分
∴AC=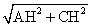 ==5,
==5,
∴此时CP=r=5;···············2分
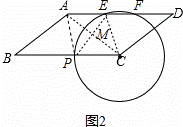 (2)如图2,若AP∥CE,APCE为平行四边形,
(2)如图2,若AP∥CE,APCE为平行四边形,
∵CE=CP,
∴四边形APCE是菱形,···········3分
连接AC、EP,则AC⊥EP,
∴AM=CM= 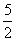 ,·········4分
,·········4分
由(1)知,AB=AC,则∠ACB=∠B,
∴CP=CE= 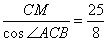 ,··········5分
,··········5分
∴EF=2 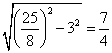 ···········6分
···········6分
(3)如图3:过点C作CN⊥AD于点N,过点A作AQ⊥BC于点Q,
∵cosB= 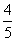
∴∠B<45°,············7分
∵∠BCG<90°,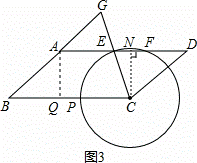
∴∠BGC>45°,············8分
∴∠BGC>∠B=∠GAE,即∠BGC≠∠GAE,
又∠AEG=∠BCG≥∠ACB=∠B=∠GAE,
∴当∠AEG=∠GAE时,A、E、G重合,则△AGE不存在.
即∠AEG≠∠GAE
∴只能∠AGE=∠AEG,············10分
∵AD∥BC,
∴△GAE∽△GBC,
∴ 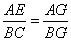 ··············11分
··············11分
即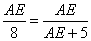 ······················12分
······················12分
解得,AE=3,EN=AN-AE=1
∴CE=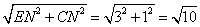 ················13分
················13分

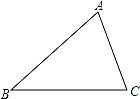
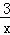 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为( )
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为( )