题目内容
2.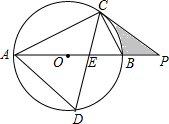 如图,AB为⊙O的直径,C为⊙O上一点,CD平分∠ACB,分别交⊙O、AB于点D,E,P为AB延长线上一点,且PC=PE.
如图,AB为⊙O的直径,C为⊙O上一点,CD平分∠ACB,分别交⊙O、AB于点D,E,P为AB延长线上一点,且PC=PE.(1)求证:PC是⊙O的切线;
(2)若⊙O的半径为3,BC:AD=1:$\sqrt{2}$,求图中阴影部分的面积;
(3)若CE:DE=1:$\sqrt{2}$,求tan∠BCP的值.
分析 (1)连接OC,由角的关系求出∠PCB=∠ACO,可得到∠OCP=90°,所以直线PC与⊙O相切.
(2)连接BD,由圆周角定理得出AD=BD,进一步得出AB=$\sqrt{2}$AD,解直角三角形求得∠BAC=30°,∠BOC=60°,从而求得PC的长,然后根据S阴影=S△POC-S扇形OBC即可求得;
(3)连接OD,作CF⊥AB于F,则OD∥CF,得出三角形相似,根据相似三角形的性质从而求得OF与半径的关系,设半径为x,则CF=OF=$\frac{\sqrt{2}}{2}$x,从而得出AF=x+$\frac{\sqrt{2}}{2}$x,解直角三角形求得tag∠BAC=$\sqrt{2}$-1,根据∠BAC=∠BCP,即可求得tan∠BCP=$\sqrt{2}$-1.
解答 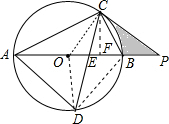 (1)证明:连接OC,
(1)证明:连接OC,
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠CAO=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
即OC⊥PC,
∴直线PC与⊙O相切.
(2)解:连接BD,
∵BC:AD=1:$\sqrt{2}$,
∴AD=$\sqrt{2}$BC,
∵AB是直径,
∴∠ACB=∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴$\widehat{AD}$=$\widehat{BD}$,
∴AD=BD,
∴△ABD是等腰直角三角形,
∴AB=$\sqrt{2}$AD,
∴AB=2BC,
∴$\frac{BC}{AB}$=$\frac{1}{2}$,
∴∠BAC=30°,
∴∠BOC=60°,
∵OC⊥PC,
∴∠P=30°,
∴OP=2OC=6,
∴PC=$\frac{\sqrt{3}}{2}$OP=3$\sqrt{3}$,
∴S阴影=S△POC-S扇形OBC=$\frac{1}{2}$×3$\sqrt{3}$×3-$\frac{60π×{3}^{2}}{360}$=$\frac{9\sqrt{3}}{2}$-$\frac{3π}{2}$;
(3)连接OD,作CF⊥AB于F,
∵AD=BD,OA=OB,
∴OD⊥AB,
∴OD∥CF,
∴$\frac{CF}{OD}$=$\frac{CE}{DE}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∵OC=OD,
∴$\frac{CF}{OC}$=$\frac{\sqrt{2}}{2}$,
∴∠COF=45°,
∴△COF是等腰直角三角形,
∴CF=OF,
设半径为x,则OA=OC=x,
∴CF=OF=$\frac{\sqrt{2}}{2}$x,
∴AF=x+$\frac{\sqrt{2}}{2}$x,
∴tag∠BAC=$\frac{CF}{AF}$=$\frac{\frac{\sqrt{2}}{2}x}{(1+\frac{\sqrt{2}}{2})x}$=$\sqrt{2}$-1,
∵∠BAC=∠BCP,
∴tan∠BCP=$\sqrt{2}$-1.
点评 本题考查了切线的判定以及扇形的面积,作出辅助线构建等腰三角形和直角三角形是解题的关键.

| A. | 3.0×105 | B. | 30×104 | C. | 3.0×104 | D. | 3.0×101 |
| A. | (x-3)(x+1) | B. | (a+2b)(2a-b) | C. | (-a+1)(-a-1) | D. | (x-3)2 |
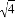 的值为( ).
的值为( ).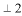 D. 4
D. 4