Question

3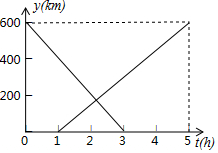．如图，A、B两地相距600km，一辆动车从A地开往B地，一辆高铁从B地开往A地，高铁先出发，一小时后，动车才出发，设动车离A地的距离为y₁（km），高铁离A地的距离为y₂（km）高铁出发时间为t（h），变量y₁，y₂之间的关系图象如图所示：
（1）根据图象，高铁和动车的速度分别是200（km/h），150（km/h）；
（2）高铁出发多少小时与动车相遇？
（3）高铁出发多长时间两车相距50km．

Answer 1

分析 （1）分别根据速度=路程÷时间列式计算即可得解；
（2）利用待定系数法求一次函数解析式解答即可；
（3）先求出两车相遇的时间为，然后分0≤x≤$\frac{15}{7}$时，$\frac{15}{7}$＜x≤5时两种情况分别列式整理即可得解．

解答 解：（1）高铁的速度为：600÷3=200（km/h），
动车的速度为：600÷4=150（km/h）．
故答案为：200（km/h），150（km/h）；

（2）设高铁的函数解析式为：y₁=kx+b，
把（0，600），（3，0）代入y₁=kx+b得：
$\left\{\begin{array}{l}{b=600}\\{3k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-200}\\{b=600}\end{array}\right.$，
则y₁=-200x+600，
同理：动车的函数解析式为：y₂=150x-150，
当动车与高铁相遇时，即-200x+600=150x-150
得：x=$\frac{15}{7}$．                          
答：高铁出发$\frac{15}{7}$小时与动车相遇；
（另解）：设高铁经过x小时与动车相遇依题意得
200x+150（x-1）=600            　　 
得：x=$\frac{15}{7}$．                    
答：高铁出发$\frac{15}{7}$小时与动车相遇；

（3）当y₁=y₂时，两车相遇，
解得x=$\frac{15}{7}$，
①0≤x≤$\frac{15}{7}$时，
y₁-y₂=-200x+600-（150x-150）=50，
得：x=2，
②$\frac{15}{7}$＜x≤5时，y₂-y₁=150x-150-（-200x+600）=50，
得：x=$\frac{16}{7}$，
综上所述：当x=2或$\frac{16}{7}$时两车相距50km．

点评 本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，路程、速度、时间三者之间的关系，（3）求出相遇的时间然后分情况讨论是难点．