题目内容
2.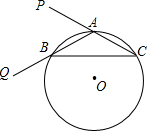 如图,在△ABC中,AB=AC,延长CA到P,延长AB到Q,使AP=BQ,求证:△ABC的外心O与A,P,Q四点共圆.
如图,在△ABC中,AB=AC,延长CA到P,延长AB到Q,使AP=BQ,求证:△ABC的外心O与A,P,Q四点共圆.
分析 先作△ABC的外接圆⊙O,并作OE⊥AB于E,OF⊥AC于F,连接OP、OQ、OB、OA,证出BE=AF,OE=OF,可证Rt△OPF≌Rt△OQE,得到∠P=∠Q即可得到答案.
解答 证明:如图,作△ABC的外接圆⊙O,作OE⊥AB于E,OF⊥AC于F,连接OP、OQ、OB、OA,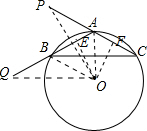
∵O是△ABC的外心,
∴OE=OF,OB=OA,
由勾股定理得:BE2=OB2-OE2,AF2=OA2-OF2,
∴BE=AF,
∵AP=BQ,
∴PF=QE,
∵OE⊥AB,OF⊥AC
∴∠OFP=∠OEQ=90°,
在Rt△OPF和Rt△OQE中,
$\left\{\begin{array}{l}{PF=QE}\\{OF=OE}\end{array}\right.$,
∴Rt△OPF≌Rt△OQE,
∴∠P=∠Q,
∴O、A、P、Q四点共圆,即:△ABC的外心O与点A、P、Q四点共圆.
点评 本题主要考查了四点共圆,涉及全等直角三角形的判定与性质及圆的有关知识,解题的关键是正确的作出辅助线得出Rt△OPF≌Rt△OQE.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.下列能判定△ABC≌△A′B′C′的是( )
| A. | AB=A′B′,BC=B′C′,∠C=∠C′ | |
| B. | ∠B=135°,∠B′=135°,AB=B′C′,BC=C′A′ | |
| C. | AB=BC=CA,A′B′=B′C′=C′A′,∠A=∠A′ | |
| D. | AB=A′B′,BC=B′C′,∠B=∠B′=135° |
11.下列调查中,适合全面调查的是( )
| A. | 了解旬河水中汞含量是否符合规定标准 | |
| B. | 了解县师训教研中心36名员工的健康状况 | |
| C. | 商家为了解某一批“电子白板”的使用寿命 | |
| D. | 为了解空气中PM2.5含量 |
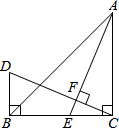 在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.
在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.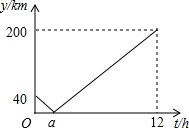 甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:
甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题: 如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.
如图所示,已知a∥b,AB⊥a,∠1=50°,∠2=65°,求∠3和∠4的度数.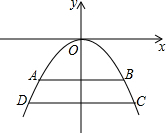 某拱桥的截面呈抛物线形,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系(如图所示),抛物线的解析式为y=-$\frac{1}{2}$x2,水面AB到拱顶O的距离为2米.
某拱桥的截面呈抛物线形,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系(如图所示),抛物线的解析式为y=-$\frac{1}{2}$x2,水面AB到拱顶O的距离为2米.