题目内容
已知圆O的直径AB与弦CD交于M，∠AMC=30°，AM=8cm，MB=2cm，求弦CD的长．
考点：垂径定理,含30度角的直角三角形,勾股定理
专题：计算题
分析：根据题意画出图形，作ON⊥CD，可得N为CD中点，连接OC，由AM+MB求出直径AB的长，进而确定出半径的长，由OB-BM求出OM的长，在直角三角形OMN中，利用30度角所对的直角边等于斜边的一半求出ON的长，在直角三角形OCN中，利用勾股定理求出CN的长，即可确定出CD的长．
解答：
解：根据题意画出图形，作ON⊥CD，可得N为CD中点，连接OC，
∵AM=8cm，MB=2cm，
∴AB=AM+BM=8+2=10cm，即OC=OB=5cm，OM=OB-MB=3cm，
在Rt△OMN中，∠AMC=30°，OM=3cm，
∴ON=
，
在Rt△ONC中，OC=5cm，ON=
，
根据勾股定理得：CN=
=
，
则CD=2CN=
．
解：根据题意画出图形，作ON⊥CD，可得N为CD中点，连接OC，∵AM=8cm，MB=2cm，
∴AB=AM+BM=8+2=10cm，即OC=OB=5cm，OM=OB-MB=3cm，
在Rt△OMN中，∠AMC=30°，OM=3cm，
∴ON=
| 3 |
| 2 |
在Rt△ONC中，OC=5cm，ON=
| 3 |
| 2 |
根据勾股定理得：CN=
52-(
|
| ||
| 2 |
则CD=2CN=
| 91 |
点评：此题考查了垂径定理，勾股定理，熟练掌握定理是解本题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
若
+（y+2）2=0，则（x+y）2014等于（ ）
| x-1 |
| A、? 1 |
| B、1 |
| C、32014 |
| D、? 32014 |
如图，四边形ABCD中，∠ACB=∠BAD=90°，AB=AD，BC=2，AC=6，四边形ABCD的面积为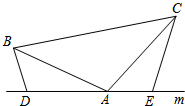
在△ABC中，AB=AC，DAE三点都在直线m上，并且有∠BDA=∠AEC=∠BAC，求证：DE=BD+CE．