题目内容
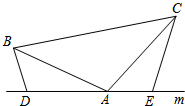 在△ABC中,AB=AC,DAE三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.
在△ABC中,AB=AC,DAE三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.考点:全等三角形的判定与性质
专题:证明题
分析:利用∠BDA=∠BAC得到:∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.
解答:证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;得出∠CAE=∠ABD是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在-(-
),-1,0,-|-4|,-(+3),+(-1
),-|0-8|这几个有理数中,负数的个数是( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、5个 | B、4个 | C、3个 | D、2个 |
当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为( )
| A、汽车的速度很快 |
| B、盲区增大 |
| C、汽车的速度很慢 |
| D、盲区减小 |
一串数:
,0,-
,0,
,0,-
,…,那么第2014个数是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
| B、0 | ||
C、-
| ||
| D、无法确定 |
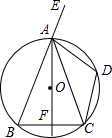 如图,⊙O是△ABC的外接圆,AO⊥BC于F,D为
如图,⊙O是△ABC的外接圆,AO⊥BC于F,D为 |
| AC |
| A、57° | B、38° |
| C、33° | D、28.5° |