题目内容
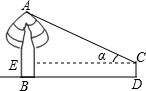 小明和小亮一起测量底部可以到达的一棵大树AB的高度,按如下步骤进行:
小明和小亮一起测量底部可以到达的一棵大树AB的高度,按如下步骤进行:①在测点D处安置测倾器,测得大树顶部的仰角∠ACE=α;
②量出测点D到大树底部B的水平距离BD=l;
③量出测倾器的高度DC=a;
他们测得了三组数据后,制成了测点到大树的距离l,测倾器的高a的数据的条形统计图(如图1)和仰角 α数据的折线统计图(如图2).
| 1 | a | α | |
| 第一次 | |||
| 第二次 | |||
| 第三次 | |||
| 平均值 |
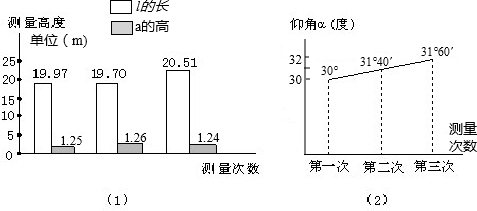
请你根据两个统计图提供的信息,完成以下任务:
(1)把统计图中的相关数据填入相应的表格中;
(2)根据得到的样本平均数计算出树高AB(精确到0.1m).
考点:解直角三角形的应用-仰角俯角问题,条形统计图,折线统计图,加权平均数
专题:阅读型,图表型
分析:(1)把折线图中的数据直接填到表中即可;
(2)分别求得三次测量的数据的平均数即可得到a、α和l的值,然后在直角三角形中利用三角函数求得AE的长,进而求得AB的长.
(2)分别求得三次测量的数据的平均数即可得到a、α和l的值,然后在直角三角形中利用三角函数求得AE的长,进而求得AB的长.
解答:解:(1)
(2)l的长是:
(19.97+19.70+20.51)=20.06(m),
a=
(1.25+1.26+1.24)=1.25)(m),
仰角α的度数是:
(30°+31°40′+31°60′)≈31°13′,
在直角△ACE中,tanα=
=
,
则AE=20.06×tan31°13′≈20.06×0.61≈12.24(m),
则AB=AE+a=12.24+1.25=13.49≈13.5(m).
故树高AB为13.5m.
| 1 | a | α | |
| 第一次 | 19.97 | 1.25 | 30° |
| 第二次 | 19.70 | 1.26 | 31°40′ |
| 第三次 | 20.51 | 1.24 | 31°60′ |
| 平均值 |
| 1 |
| 3 |
a=
| 1 |
| 3 |
仰角α的度数是:
| 1 |
| 3 |
在直角△ACE中,tanα=
| AE |
| EC |
| AE |
| l |
则AE=20.06×tan31°13′≈20.06×0.61≈12.24(m),
则AB=AE+a=12.24+1.25=13.49≈13.5(m).
故树高AB为13.5m.
点评:本题考查解直角三角形的方法以及样本平均数,分清题意正确求得a、α和l的值是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一元二次方程x(x-2)=2-x的根是( )
| A、x=-1 |
| B、x=2 |
| C、x1=1,x2=2 |
| D、x1=-1,x2=2 |
 全世界每年都有大量的土地被沙漠吞没,改造沙漠,保护土地资源已称为一项十分紧迫的任务.某地元有沙漠100万公顷,为了了解该地区沙漠面积的变化情况,有关部门进行了连续3年的观察,并将每年年底的观察结果坐了记录(如下表所示),然后根据这些数据描点、连线,绘成曲线图如图所示,发现其连续且成直线状.预计该地区的沙漠面积将继续按此趋势扩大.
全世界每年都有大量的土地被沙漠吞没,改造沙漠,保护土地资源已称为一项十分紧迫的任务.某地元有沙漠100万公顷,为了了解该地区沙漠面积的变化情况,有关部门进行了连续3年的观察,并将每年年底的观察结果坐了记录(如下表所示),然后根据这些数据描点、连线,绘成曲线图如图所示,发现其连续且成直线状.预计该地区的沙漠面积将继续按此趋势扩大. 在平面直角坐标系中描出下列各点.
在平面直角坐标系中描出下列各点. (1)在图中画出函数y=2x-1的图象;
(1)在图中画出函数y=2x-1的图象;