题目内容
一元二次方程x（x-2）=2-x的根是（ ）
| A、x=-1 |
| B、x=2 |
| C、x1=1，x2=2 |
| D、x1=-1，x2=2 |
考点：解一元二次方程-因式分解法
专题：计算题,转化思想
分析：先移项得到x（x-2）+（x-2）=0，然后利用因式分解法解方程．
解答：解：x（x-2）+（x-2）=0，
（x-2）（x+1）=0，
x-2=0或x+1=0，
所以x1=2，x2=-1．
故选D．
（x-2）（x+1）=0，
x-2=0或x+1=0，
所以x1=2，x2=-1．
故选D．
点评：本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
灵星计算小达人系列答案
相关题目
下列不等式x≤-1的解集，表示正确的是（ ）
A、 |
B、 |
C、 |
D、 |
若x＜y，下列式子中不成立的是（ ）
| A、-x＞-y | ||||
| B、3x-2＜3y-2 | ||||
| C、-2x+1＞-2y+1 | ||||
D、-
|
方程x2-3|x-1|=1的不同解的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
下列数据不能确定目标的位置是（ ）
| A、教室内的3排2列 |
| B、东经100°北纬45° |
| C、永林大道12号 |
| D、南偏西40° |
不等式3x-2≤4（x-1）的解集为（ ）
| A、x≥2 | B、x≤2 |
| C、x≥-2 | D、x≤-2 |
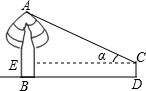小明和小亮一起测量底部可以到达的一棵大树AB的高度，按如下步骤进行：