题目内容
13. 如图,在矩形ABCD中,AB=4cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B;点P出发几秒后,点P、A的距离是点P、C距离的$\sqrt{3}$倍?
如图,在矩形ABCD中,AB=4cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B;点P出发几秒后,点P、A的距离是点P、C距离的$\sqrt{3}$倍?
分析 设点P出发x秒后,点P、A的距离是点P、C的距离的$\sqrt{3}$倍,分别表示出PA、PC的长度,然后根据题意列出方程,求解方程.
解答 解:设点P出发x秒后,点P、A的距离是点P、C的距离的$\sqrt{3}$倍,
则PA=x,PC=$\sqrt{B{C}^{2}+P{B}^{2}}$=$\sqrt{2+(4-x)^{2}}$,
由题意得,x=$\sqrt{3}$×$\sqrt{2+(4-x)^{2}}$,
整理得到:(x-9)(x-3)=0,
解得:x1=9(不合题意,舍去),x2=3,
答:点P出发3秒后,点P、A的距离是点P、C的距离的$\sqrt{3}$倍.
点评 本题考查了一元二次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
2. 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )| A. | BD=AD | B. | AB=AC | C. | ∠1=∠2 | D. | 以上答案都不对 |
3. 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )| A. | a>b | B. | ab<0 | C. | b-a>0 | D. | a+b>0 |

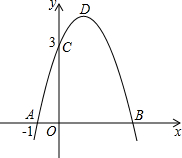 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为A(-1,0),另一交点为B,与y轴的交点坐标为C(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为A(-1,0),另一交点为B,与y轴的交点坐标为C(0,3). 如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长.
如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长. 如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E. 求∠DBC的度数.
如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E. 求∠DBC的度数.