题目内容
1.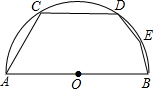 如图,在半圆中AB为直径,弦AC=CD=6$\sqrt{2}$,DE=EB=2,弧CDE的长度为$\frac{5\sqrt{2}}{2}π$.
如图,在半圆中AB为直径,弦AC=CD=6$\sqrt{2}$,DE=EB=2,弧CDE的长度为$\frac{5\sqrt{2}}{2}π$.
分析 过点E作EH⊥CD于H,连接OC、OE、AE,如图所示.根据弧、弦和圆周角的关系可得∠COE=90°,根据圆周角定理可得∠CAE=45°,再根据圆内接四边形对角互补及同角的补角相等可得∠HDE=45°,然后运用勾股定理可依次求出CE,CO,然后运用圆弧长公式就可解决问题.
解答 解:过点E作EH⊥CD于H,连接OC、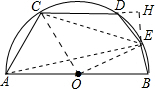 OE、AE,如图所示.
OE、AE,如图所示.
∵AC=CD,DE=EB,
∴$\widehat{AC}=\widehat{CD}$,$\widehat{DE}=\widehat{BE}$,
∴∠COE=$\frac{1}{2}$∠AOB=90°,
∴∠CAE=45°.
∵∠CDE+∠CAE=180°,∠CDE+∠HDE=180°,
∴∠HDE=∠CAE=45°.
在Rt△DHE中,HE=DE•sin∠HDE=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
DH=DE•cos∠HDE=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
在Rt△CHE中,CE=$\sqrt{C{H}^{2}+H{E}^{2}}$=$\sqrt{(6\sqrt{2}+\sqrt{2})^{2}+(\sqrt{2})^{2}}$=10.
在Rt△COE中,CO=$\frac{\sqrt{2}}{2}$CE=5$\sqrt{2}$,
∴弧CDE的长度为$\frac{90π•5\sqrt{2}}{180}$=$\frac{5\sqrt{2}}{2}π$.
故答案为$\frac{5\sqrt{2}}{2}π$.
点评 本题主要考查了等弧与等弦及等圆心角之间的关系、圆周角定理、圆内接四边形的对角互补、特殊角的三角函数值、勾股定理、圆弧长公式等知识,通过解三角形CDE求出CE,进而求出半径,是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 22015 | B. | 22014 | C. | -22014 | D. | 3×22014 |
| A. | y=$\frac{1}{2}$x2 | B. | y=(x+0.5)2+2 | C. | y=(x-0.5)2+2 | D. | y=x2-2x-0.5 |
 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠EAD的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠EAD的度数.