题目内容
20.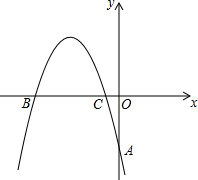 如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4),B(x1,0),C(x2,0)三点,且|x2-x1|=5.
如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4),B(x1,0),C(x2,0)三点,且|x2-x1|=5.(1)求b,c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
分析 (1)把A(0,-4)代入可求c,运用两根关系及|x2-x1|=5,对式子合理变形,求b;
(2)因为菱形的对角线互相垂直平分,故菱形的另外一条对角线必在抛物线的对称轴上,满足条件的D点,就是抛物线的顶点;
(3)由四边形BPOH是以OB为对角线的菱形,可得PH垂直平分OB,求出OB的中点坐标,代入抛物线解析式即可,再根据所求点的坐标与线段OB的长度关系,判断是否为正方形即可.
解答 解:(1)∵抛物线y=-$\frac{2}{3}$x2+bx+c,经过点A(0,-4),
∴c=-4
又∵由题意可知,x1、x2是方程-$\frac{2}{3}$x2+bx-4=0的两个根,
∴x1+x2=$\frac{3}{2}$b,x1x2=6
由已知得(x2-x1)2=25
又∵(x2-x1)2=(x2+x1)2-4x1x2=$\frac{9}{4}$b2-24
∴$\frac{9}{4}$b2-24=25
解得b=±$\frac{14}{3}$,当b=$\frac{14}{3}$时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.
∴b=-$\frac{14}{3}$.
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,
又∵y=-$\frac{2}{3}$x2-$\frac{14}{3}$x-4=-$\frac{2}{3}$(x+$\frac{7}{2}$)2+$\frac{25}{6}$,
∴抛物线的顶点(-$\frac{7}{2}$,$\frac{25}{6}$)即为所求的点D.
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),根据菱形的性质,点P必是直线x=-3与
抛物线y=-$\frac{2}{3}$x2-$\frac{14}{3}$x-4的交点,
∴当x=-3时,y=-$\frac{2}{3}$×(-3)2-$\frac{14}{3}$×(-3)-4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形.
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上
点评 本题考查了抛物线解析式的求法,根据菱形,正方形的性质求抛物线上符合条件的点的方法.

 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 已知有理数a,b,c在数轴上的位置如图所示,试用“>”将有理数a,-a,b,-b,c,-c,0连接起来.
已知有理数a,b,c在数轴上的位置如图所示,试用“>”将有理数a,-a,b,-b,c,-c,0连接起来.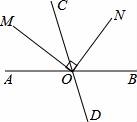
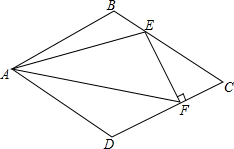 菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.