题目内容
4．若△ABC的三边a，b，c满足2a2+b2-12a-8b+$\sqrt{25-10c+{c}^{2}}$=-34，判断三角形的形状．分析 把等式右边的项移到左边，根据字母a、b的系数把常数项34分成18、16，然后与（2a2-12a）、（b2-8b）分别组成完全平方公式，25-10c+c2=（5-c）2，再利用非负数的性质，可分别求出a、b、c的值，然后利用勾股定理判定三角形的形状即可．
解答 解：∵2a2+b2-12a-8b+$\sqrt{25-10c+{c}^{2}}$=-34，
∴（2a2-12a+18）+（b2-8b+16）+$\sqrt{（5-c）^{2}}$=0，
∴2（a-3）2+（b-4）2+$\sqrt{（5-c）^{2}}$=0，
∴a-3=0，b-4=0，5-c=0，
∴a=3，b=4，c=5，
∵32+42=52，
∴△ABC是直角三角形．
点评 此题考查了配方法的应用、勾股定理、非负数的性质，解题的关键是注意配方法的步骤，在变形的过程中不要改变式子的值．
练习册系列答案
名师点拨卷系列答案
相关题目
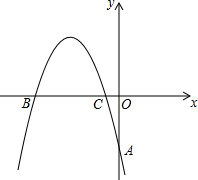如图，在平面直角坐标系中，抛物线y=-$\frac{2}{3}$x2+bx+c，经过A（0，-4），B（x1，0），C（x2，0）三点，且|x2-x1|=5．
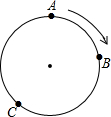上海世博园中，有A、B、C三个国家的展馆由一个圆形通道相连，小明在参观游览过程中发现，沿顺时针方向走，从A馆到C馆要12分钟，从B馆到A馆要15分钟，从C馆到B馆要11分钟，你能求出从A馆到B馆需要多少分钟吗？
，求
的值。（先化简再求值）