题目内容
16.某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-$\frac{1}{20}$x2+5(长度单位:m)(1)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(2)在拱桥加固维修时,在高度为1.8m及以上时,需搭建的“脚手架”,“脚手架”横截面为矩形EFGH(E,F在AB上,H、G分别在抛物线的左右侧上,高FG≥1.8m),求“脚手架”横截面所在矩形EFGH的最大周长.
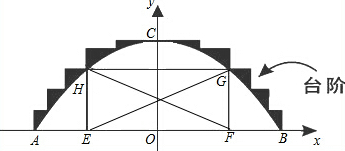
分析 (1)根据解析式求出A,B,C三点坐标,求出地毯的总长度,再根据地毯的价格求出购买地毯需要的钱.
(2)利用HE=FG=y=-$\frac{1}{20}$x2+5,GH=EF=2x,即可得出HE+FG+2GH与x的函数关系,进而求出最值即可.
解答 解:(1)由y=-$\frac{1}{20}$x2+5知,OC=5m,
令y=0,即y=-$\frac{1}{20}$x2+5=0,
解得x1=10,x2=-10(舍去);
∴地毯的总长度为:AB+2OC=20+2×5=30m,
∴30×1.5×20=900元
答:购买地毯需要900元.
(2)设F(x,0)则G(x,-$\frac{1}{20}$x2+5),
∴HE=FG=-$\frac{1}{20}$x2+5,GH=EF=2x,
∴HE+FG+GH+EF=-$\frac{1}{10}$x2+10+4x
=-$\frac{1}{10}$(x-20)2+50(0<x≤8),
∵-$\frac{1}{10}$<0,
∴x=8时有最大值为35.6.
答:“脚手架”横截面所在矩形EFGH的最大周长是35.6m.
点评 本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=$-\frac{b}{2a}$时取得.

练习册系列答案
相关题目
4.《国家园林城市创建标准》规定:绿化率(绿地面积占土地面积)为31%,绿化覆盖率(绿化覆盖面积占土地面积)为36%,人均公共绿地为7.5平方米,据调查淮安市区绿化情况如表:
(1)淮安市区绿化率是多少?达标吗?
(2)淮安市人均公共绿地比国家园林城市规定标准少百分之几?
(3)市区将新建一处占地面积为12000平方米的居民小区,小区内绿化覆盖面积至少是多少平方米才能达到国家规定标准?
| 项目 | 土地面积 | 绿地面积 | 绿化覆盖率 | 人均公共绿地 |
| 数据 | 1500平方千米 | 450平方千米 | 38% | 7.2平方米 |
(2)淮安市人均公共绿地比国家园林城市规定标准少百分之几?
(3)市区将新建一处占地面积为12000平方米的居民小区,小区内绿化覆盖面积至少是多少平方米才能达到国家规定标准?
5.在Rt△ABC中,若各边的长度都扩大2倍,则锐角A的四个三角比值( )
| A. | 也扩大2倍 | B. | 缩小为$\frac{1}{2}$倍 | ||
| C. | 都不变 | D. | 有的扩大,有的缩小 |
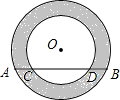 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C、D两点.
如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C、D两点. 如图,在平面直角坐标系中,O为坐标原点,B的坐标(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°
如图,在平面直角坐标系中,O为坐标原点,B的坐标(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°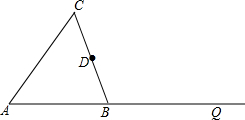 如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
如图,△ABC是等腰三角形,AB=BC,点D为BC的中点. 一个正方体的每个面都写着一个汉字,其平面展开图如图所示,那么在该正方体中,和“曲”相对的汉字是( )
一个正方体的每个面都写着一个汉字,其平面展开图如图所示,那么在该正方体中,和“曲”相对的汉字是( )