题目内容
9.如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,求证△GEF是等腰直角三角形;
(3)如图3,若AB=2$\sqrt{3}$,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.

分析 (1)根据矩形的性质得到∠EAM=∠FDM=90°,根据全等三角形的判定定理得到△AEM≌△DFM(ASA),由全等三角形的性质即可得到结论;
(2)过点G作GH⊥AD于H,推出四边ABGH为矩形,得到∠AME+∠AEM=90°,由于∠AME+∠GMH=90°等量代换得到∠AEM=∠GMH,推出△AEM≌△HMG(AAS),根据全等三角形的性质得到ME=MG,求得∠EGM=45°.根据全等三角形的性质得到ME=MF.即可得到结论;
(3 )根据四边形ABCD是矩形,得到∠A=∠ADC=90°,等量代换得到∠AEM=∠DMC,根据相似三角形的性质得到$\frac{AE}{MD}=\frac{AM}{CD}$,代入数据求得AE=$\frac{2\sqrt{3}}{3}$,当E、B重合时,AE最长为2$\sqrt{3}$,于是得到结论.
解答 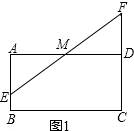 (1)证明:如图1,在矩形ABCD中,∠EAM=∠FDM=90°,
(1)证明:如图1,在矩形ABCD中,∠EAM=∠FDM=90°,
∵M是AD的中点,
∴AM=DM,
又∠AME=∠FMD,
在△AEM与△DFM中,$\left\{\begin{array}{l}{∠EAM=∠FDM}\\{AM=DM}\\{∠AME=∠DMF}\end{array}\right.$,
∴△AEM≌△DFM(ASA),
∴AE=DF;
(2)证明:如图2,过点G作GH⊥AD于H,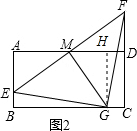
∴∠A=∠B=∠AHG=90°,
∴四边ABGH为矩形,
∴∠AME+∠AEM=90°,
∵MG⊥EF,
∴∠GME=90°.
∴∠AME+∠GMH=90°
∴∠AEM=∠GMH,
∵AD=4,M是AD的中点,
∴AM=2,
∵四边ABGH为矩形,
∴AB=HG=2,
∴AM=HG,
在△AEM与△HMG中,$\left\{\begin{array}{l}{∠A=∠MHG=90°}\\{∠AEM=∠HMC}\\{AM=HG}\end{array}\right.$,
∴△AEM≌△HMG(AAS),
∴ME=MG,
∴∠EGM=45°.
由(1)得△AEM≌△DFM,
∴ME=MF.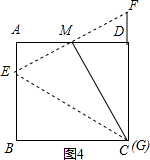
∵MG⊥EF,
∴GE=GF,
∴∠EGF=2∠EGM=90°.
∴△GEF是等腰直角三角形;
(3 )解:当C、G重合时,如图4,
∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠AME+∠AEM=90°.
∵MG⊥EF,
∴∠EMG=90°,
∴∠AME+∠DMC=90°,
∴∠AEM=∠DMC,
∴△AEM∽△DMC
∴$\frac{AE}{MD}=\frac{AM}{CD}$,
∴$\frac{AE}{2}=\frac{2}{2\sqrt{3}}$,
∴AE=$\frac{2\sqrt{3}}{3}$,
当E、B重合时,AE最长为2$\sqrt{3}$,
∴$\frac{2\sqrt{3}}{3}$<AE≤2$\sqrt{3}$.
点评 本题考查了全等三角形的判定和性质,矩形的判定和性质,相似三角形的判定和性质,等腰直角三角形的判定,正确的作出辅助线构造全等三角形是解题的关键.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案| 筹款金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
| 人数 | 3 | 7 | 11 | 11 | 13 | 5 |
| A. | 11,20 | B. | 25,11 | C. | 20,25 | D. | 25,20 |
| A. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| B. | “抛一枚硬币,正面朝上的概率为$\frac{1}{2}$”,表示每抛两次就有一次正面朝上 | |
| C. | “抛一枚均匀的正方体骰子,朝上的点数是6的概率为$\frac{1}{6}$”,表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的概率稳定在$\frac{1}{6}$附近 | |
| D. | 某种彩票的中奖概率为$\frac{1}{1000}$,说明每买1000张,一定有一张中奖 |
 如图,有一块三角形材料(△ABC),请用尺规画出△ABC的外接圆.(不写作法,保留作图痕迹)
如图,有一块三角形材料(△ABC),请用尺规画出△ABC的外接圆.(不写作法,保留作图痕迹)