题目内容
已知，如图，在△ABC中，∠ABC=68°，∠ACB=50°，BE、CF是两边AC、AB上的高，它们交于点H．求∠BHC的度数．
考点：三角形内角和定理
专题：计算题
分析：先根据三角形内角和定理计算出∠A=180°-∠ABC-∠ACB=62°，再根据高的定义得∠AEB=∠AFC=90°，于是利用四边形内角和为360°可计算出∠EHF=118°，然后根据对顶角相等得到∠BHC的度数．
解答：解：∵∠ABC=68°，∠ACB=50°，
∴∠A=180°-∠ABC-∠ACB=62°，
∵BE、CF是两边AC、AB上的高，
∴∠AEB=∠AFC=90°，
而∠A+∠AFH+∠AEH+∠EHF=360°，
∴∠EHF=180°-62°=118°，
∴∠BHC=118°．
∴∠A=180°-∠ABC-∠ACB=62°，
∵BE、CF是两边AC、AB上的高，
∴∠AEB=∠AFC=90°，
而∠A+∠AFH+∠AEH+∠EHF=360°，
∴∠EHF=180°-62°=118°，
∴∠BHC=118°．
点评：本题考查了三角形内角和定理：三角形内角和是180°．注意角的运算．
练习册系列答案
名校课堂系列答案
相关题目
如图，请你数出五角星中同旁内角的对数．等腰三角形中，已知两边的长分别是9和4，则周长为（ ）
| A、17 | B、22 |
| C、17或22 | D、以上答案都不对 |
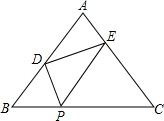如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，且BP=2，将一个大小与∠B相等的角的顶点放在P 点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E．