题目内容
 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且
(1)直接写出B点坐标;
(2)若过点C的直线CD交AB边于点D,且把矩形OABC的周长分为1:3两部分,求直线CD的解析式.
解:(1) ,
,
a=3,b=5,
矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),
∴B点坐标是(3,5);
(2)如图: 设D点坐标是(3,y),
设D点坐标是(3,y),
CBD的周长:ADCO的周长=1:3,
[3+(5-y)]:(5+3++y)=1:3
y=4,
D点坐标是(3,4)
设CD的解析式为y=kx+b (k是常数b,是常数k≠0),
CD经过C、D点,

把①代入②得,
k=- ,
,
直线CD的解析式为y=- x+b.
x+b.
分析:(1)根据平方与算术平方根的和为0,可得平方与算术平方跟同时为0,可得a、b的值,根据矩形,可得B点的坐标;
(2)根据周长的比,可得D点的坐标,根据待定系数法求解析式,可得答案.
点评:本题考查了一次函数的综合题,(1)先求出a、b的值,可得B点的坐标;(2)先根据周长的比求出D点的坐标,再用待定系数法求出函数解析式.
 ,
,a=3,b=5,
矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),
∴B点坐标是(3,5);
(2)如图:
 设D点坐标是(3,y),
设D点坐标是(3,y),CBD的周长:ADCO的周长=1:3,
[3+(5-y)]:(5+3++y)=1:3
y=4,
D点坐标是(3,4)
设CD的解析式为y=kx+b (k是常数b,是常数k≠0),
CD经过C、D点,

把①代入②得,
k=-
 ,
,直线CD的解析式为y=-
 x+b.
x+b.分析:(1)根据平方与算术平方根的和为0,可得平方与算术平方跟同时为0,可得a、b的值,根据矩形,可得B点的坐标;
(2)根据周长的比,可得D点的坐标,根据待定系数法求解析式,可得答案.
点评:本题考查了一次函数的综合题,(1)先求出a、b的值,可得B点的坐标;(2)先根据周长的比求出D点的坐标,再用待定系数法求出函数解析式.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
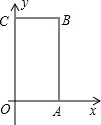 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5). 17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为
17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为

 如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )
如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )