题目内容
16.如图,4×4方格中每个小正方形的边长都为1.(1)图1中正方形ABCD的面积为5,边长为$\sqrt{5}$.
(3)在图2的4×4方格中,画一个面积为8的格点正方形(四个顶点都在方格的顶点上).
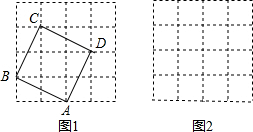
分析 (1)由勾股定理求出正方形ABCD的面积=AB2=12+22=5,即可得出边长AB=$\sqrt{5}$;
(2)由勾股定理求出面积为8的正方形的边长=2$\sqrt{2}$,化成正方形即可.
解答  解:(1)正方形ABCD的面积=AB2=12+22=5,
解:(1)正方形ABCD的面积=AB2=12+22=5,
边长AB=$\sqrt{5}$;
故答案为:5,$\sqrt{5}$;
(2)面积为8的正方形的边长=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
面积为8的正方形如图所示.
点评 本题考查了勾股定理、正方形的性质;熟练掌握正方形的性质,由勾股定理求出正方形的面积好边长是解决问题的关键.

练习册系列答案
相关题目
4.如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为( )
| A. | 1 | B. | 4 | C. | 8 | D. | 16 |
8.永川重百商场为庆祝“元旦”,特搞促销活动,有两件进价不同的衣服均卖了80元,其中一件盈利60%,另一件亏本20%,这次买卖交易中商家( )
| A. | 不赔不赚 | B. | 赚了8元 | C. | 赚了10元 | D. | 赚了32元 |
 如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一个动点(不与A、B重合),作EF⊥AB交边BC于点F,联结AF、EC交于点G.
如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一个动点(不与A、B重合),作EF⊥AB交边BC于点F,联结AF、EC交于点G.