题目内容
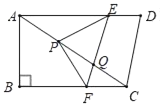
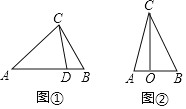
【题目】如图①在![]() 中,若点
中,若点![]() 在边
在边![]() 上,且
上,且![]() 则点
则点![]() 定义为
定义为![]() 的边
的边![]() 上的“金点”.
上的“金点”.
![]() 已知点
已知点![]() 是
是![]() 的边
的边![]() 上的“金点”:
上的“金点”:
①若![]() 则
则![]() 的长为 _;
的长为 _;
②若![]() 则
则![]() 的长为 _;
的长为 _;
![]() 在图①中,若点
在图①中,若点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 试判断点
试判断点![]() 是不是
是不是![]() 的“金
的“金
点”,并说明理由;
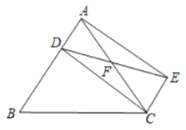
![]() 如图②,已知点
如图②,已知点![]() 为同一直线上三点,且
为同一直线上三点,且![]() 在
在![]() 所在直线上是否存在一点
所在直线上是否存在一点![]() 使点
使点![]() 中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段
中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)①![]() 或
或![]() ; ②
; ②![]() ;(2)点
;(2)点![]() 是
是![]() 的“金点”,理由见解析;(3)存在,满足条件的
的“金点”,理由见解析;(3)存在,满足条件的![]() 长为
长为![]() 或
或![]() .
.
【解析】
(1)①分两种情形,利用相似三角形的性质解决问题即可.②利用相似三角形的性质解决问题即可.
(2)结论:点D是△ABC的“金点”.只要证明△ACD∽△ABC即可解决问题;
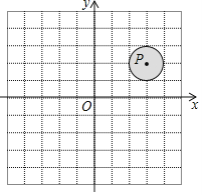
(3)如图③中,存在.有三种情形:过点A作MA⊥AC交CB的延长线于M,作MH⊥y轴于H.构造全等三角形,利用平行线分线段成比例定理构建方程求出点C坐标,分三种情形求解即可解决问题;
(1)![]() 若
若![]() 如图:
如图:

∵![]()
∴![]() .
.
∴![]()
∴![]()
∴![]()
若![]() 如图:
如图:
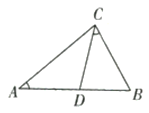
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
![]() 如图所示:
如图所示:
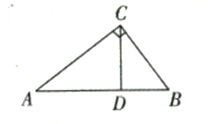
∵点![]() 是
是![]() 的“金点”,
的“金点”,
∴![]() 或
或![]()
当![]() 时,
时,
∵![]()
∴![]()
∴![]() ;
;
当![]() 时,
时,
同理可证![]() .
.
在![]() 中,由勾股定理得,
中,由勾股定理得,
![]()
∵![]()
∴![]()
故答案为:①![]() 或
或![]() ; ②
; ②![]() ;
;
(2)点![]() 是
是![]() 的“金点”,
的“金点”,
理由如下:
∵点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]()
∴![]()
又∵![]()
∴![]()
![]()
∴![]()
又![]()
![]()
∴![]()
所以点![]() 是
是![]() 的“金点”;
的“金点”;
故答案为:点![]() 是
是![]() 的“金点”,理由见解析.
的“金点”,理由见解析.
(3)存在.
有三种情形:
如图所示:过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]() .
.
设![]()
∵![]()
∴![]()
∵![]()
∵![]() .
.
∴![]()
∴![]()
解得![]() 或
或![]() (舍去),
(舍去),
∴![]()
![]() 当
当![]() 时,点
时,点![]() 是
是![]() 的“金点”设
的“金点”设![]()
∵![]() ,
,
∴![]()
∴![]() ,即
,即![]() .
.
∴![]() ,
,
解得![]()
∴![]() .
.
![]() 当
当![]() 时,点
时,点![]() 是
是![]() 的“金点”
的“金点”
易知![]() ,
,
∴![]() .
.
![]() 当
当![]() 时,点
时,点![]() 是
是![]() 的“金点”
的“金点”
易知![]() ,
,
∴![]() .
.
综上所述,满足条件的![]() 长为
长为![]() 或
或![]() .
.
故答案为:存在,OD长为42或6

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】为加强公民节电意识,某县将居民用电量分为两个阶梯,月用电量不超过![]() 度时按第一个阶梯费用收费,超过
度时按第一个阶梯费用收费,超过![]() 度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 3月 |
用电量 |
|
金额 |
|
2019年3月收费员林云
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 4月 |
用电量 |
|
金额 |
|
2019年4月收费员林云