题目内容
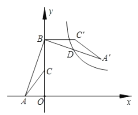
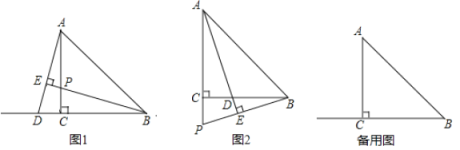
【题目】如图所示，直线y1=﹣
x与双曲线y=
交于A，B两点，点C在x轴上，连接AC，BC．当AC⊥BC，S△ABC=15时，求k的值为（ ）
A.﹣10B.﹣9C.6D.4
【答案】B
【解析】
先根据正比例函数和反比例函数的性质得到点
与点
关于原点对称，
，再根据直角三角形斜边上的中线性质得到
，设
，则
，利用勾股定理表示出
，则
，接着利用三角形面积公式得到
，解出
得到
，
，然后把，代入
中可求出
的值．
解：∵直线y1=﹣
x与双曲线y=
交于A，B两点，
∴点A与点B关于原点对称，OA=OB，
∵AC⊥BC，
∴∠ACB=90°，
∴OA=OB=OC，
设A（t，﹣t），则B（﹣t， t），
∴OA=
=﹣
t，
∴OC=﹣t，
∵S△ABC=15，
∴
×（﹣t）（﹣t﹣）=15，解得t=﹣
，
∴A（﹣，2
），
把A（﹣，2）代入y=得k=﹣×2=﹣9．
故选：B．
练习册系列答案
相关题目
